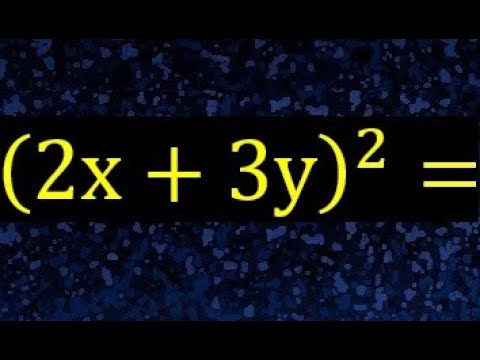Entendiendo la expresión matemática
En el ámbito matemático, el desarrollo de la expresión (2x+3y)2 nos lleva a un proceso de multiplicación y simplificación que puede resultar en un término altamente complejo. Analizar este desarrollo nos permitirá comprender con claridad cómo se obtiene el resultado final y cómo puede aplicarse en diferentes contextos matemáticos y científicos.
La importancia del desarrollo de expresiones matemáticas
El desarrollo de expresiones matemáticas es fundamental en numerosas áreas de la ciencia y la ingeniería. Permite simplificar ecuaciones, encontrar soluciones a problemas complejos y facilita la comprensión de fenómenos naturales y artificiales. En el caso específico de la expresión (2x+3y)2, su desarrollo nos brinda un insight único sobre la forma en que se comportan y operan las variables involucradas.
Componentes de la expresión (2x+3y)2
Para comenzar el desarrollo de la expresión (2x+3y)2, es crucial comprender todos los componentes que la integran. En este caso, la expresión consta de dos términos: 2x y 3y, los cuales se encuentran dentro de un paréntesis y están elevados al cuadrado. Esta particular configuración nos ofrece un desafío matemático intrigante que requerirá de pasos precisos para su resolución.
Pasos para desarrollar la expresión (2x+3y)2
El primer paso en el desarrollo de la expresión (2x+3y)2 consiste en aplicar la regla del cuadrado de un binomio. Llevar a cabo esta operación implica multiplicar el binomio por sí mismo, lo que resultará en una serie de productos que deberán sumarse posteriormente.
Primer paso: Calcular el cuadrado del primer término
El cuadrado del primer término, 2x, se obtiene multiplicándolo por sí mismo: (2x) * (2x) = 4×2.
Segundo paso: Calcular el producto cruzado
El producto cruzado implica multiplicar el primer término por el segundo término, y luego duplicar el resultado. En este caso, obtenemos: 2x * 3y = 6xy. Duplicando este resultado: 2 * 6xy = 12xy.
Tercer paso: Calcular el cuadrado del segundo término
El cuadrado del segundo término, 3y, se calcula de manera similar al primer paso: (3y) * (3y) = 9y2.
Cuarto paso: Sumar los resultados obtenidos
Finalmente, sumamos los resultados de los tres pasos anteriores: 4×2 + 12xy + 9y2. Esta suma representa el desarrollo completo de la expresión (2x+3y)2.
Aplicaciones prácticas del resultado
Una vez que hemos completado el desarrollo de la expresión (2x+3y)2, podemos explorar cómo este resultado puede aplicarse en diferentes contextos. Desde la resolución de ecuaciones en física hasta la simplificación de expresiones algebraicas en ingeniería, el desarrollo de esta expresión tiene implicaciones significativas.
Interpretación geométrica
Una interesante forma de contextualizar el resultado del desarrollo de la expresión (2x+3y)2 es a través de una interpretación geométrica. Esta expresión puede ser representada como un área en un plano cartesiano, donde los términos 2x y 3y corresponden a las dimensiones de un rectángulo, y el desarrollo (4×2 + 12xy + 9y2) constituye el área total.
Significado en términos de variables
Otra perspectiva valiosa para comprender el resultado del desarrollo de la expresión (2x+3y)2 es analizar su significado en términos de las variables involucradas. Este desarrollo nos ofrece información acerca de cómo se relacionan y combinan las variables x e y en un contexto algebraico, lo cual es relevante en la resolución de ecuaciones y la representación gráfica de funciones.
Relación con el binomio de Newton
El desarrollo de la expresión (2x+3y)2 guarda una estrecha relación con el binomio de Newton, una fórmula que permite expandir potencias de binomios. Al comprender esta relación, podemos apreciar cómo el desarrollo de la expresión se enmarca dentro de un marco teórico más amplio que abarca diversas aplicaciones matemáticas y científicas.
Aplicaciones en física y química
En campos como la física y la química, el desarrollo de expresiones matemáticas como (2x+3y)2 es fundamental para modelar fenómenos naturales, calcular energías potenciales, y resolver ecuaciones diferenciales. Este resultado concreto puede ser empleado en la determinación de distribuciones de cargas eléctricas, la formulación de leyes cinéticas, y la representación matemática de movimientos ondulatorios.
Innovaciones en ingeniería
En el contexto de la ingeniería, el desarrollo de expresiones matemáticas juega un papel crucial en la optimización de diseños, la predicción de comportamientos estructurales, y el análisis de circuitos eléctricos y electrónicos. Entender y aplicar el resultado del desarrollo de la expresión (2x+3y)2 proporciona a los ingenieros herramientas para resolver problemas complejos en áreas que van desde la ingeniería mecánica hasta la ingeniería de software.
El proceso de desarrollo de la expresión (2x+3y)2 nos ha llevado a explorar una serie de pasos y conceptos matemáticos que tienen aplicaciones extendidas en diversos campos del conocimiento. Desde su interpretación geométrica hasta su relevancia en física, química, ingeniería, y otras disciplinas, este resultado revela la conexión profunda entre la teoría matemática y su aplicación práctica.
En conclusión, el resultado del desarrollo de la expresión (2x+3y)2 representa un punto de partida para comprender la importancia de la manipulación algebraica y su impacto en la resolución de problemas complejos en ciencia y tecnología. Este proceso no solo nos brinda un resultado específico, sino que también nos abre las puertas a un universo de aplicaciones y conexiones interdisciplinarias que enriquecen nuestro entendimiento del mundo que nos rodea.