El signo de la pendiente de una recta en el plano cartesiano es un concepto fundamental en el estudio de las ecuaciones lineales. La pendiente de una recta se expresa típicamente como el cociente entre el cambio en la coordenada y (Δy) y el cambio correspondiente en la coordenada x (Δx). En el contexto de la ecuación general de una recta ax+by+c=0, la determinación del signo de la pendiente y su relación con el valor de los coeficientes a, b y c es de gran importancia en diversos campos de las matemáticas y la física.
En este artículo, exploraremos en detalle el significado del signo de la pendiente de la recta en el contexto de la ecuación general ax+by+c=0 y su relación con los valores positivos y negativos. Además, analizaremos cómo estos conceptos se aplican en la interpretación geométrica y algebraica de las rectas en el plano, brindando ejemplos ilustrativos y claros para una comprensión integral.
¿Qué es la pendiente de una recta y cómo se relaciona con la ecuación general ax+by+c=0?
Antes de adentrarnos en el análisis del signo de la pendiente, es fundamental comprender la noción de pendiente de una recta. En términos simples, la pendiente de una recta es una medida de su inclinación o la tasa de cambio que indica cómo se inclina la recta con respecto al eje horizontal en el plano cartesiano.
La relación entre la pendiente y la ecuación general de la recta ax+by+c=0 radica en el hecho de que la pendiente está intrínsecamente relacionada con los coeficientes a y b en la ecuación. Específicamente, la pendiente m se expresa en función de -a/b, donde ‘a’ y ‘b’ son los coeficientes de x e y, respectivamente. Esta relación es esencial para comprender cómo el signo de la pendiente se relaciona con los valores de los coeficientes y su impacto en la configuración de la recta en el plano.
Signo de la pendiente de la recta y su interpretación geométrica
El signo de la pendiente de una recta es un indicador crucial de su dirección en el plano cartesiano. Cuando la pendiente es positiva, la recta tiende a inclinarse hacia arriba desde izquierda a derecha, lo que implica un aumento en el valor de y a medida que x aumenta. En contraste, una pendiente negativa señala una inclinación descendente de la recta, lo que implica una disminución en y a medida que x aumenta.
Este fenómeno puede visualizarse geométricamente como una recta que sube o baja a medida que se mueve a lo largo del eje x, lo que proporciona una comprensión intuitiva del comportamiento de la pendiente en relación con el plano. Es importante destacar estas interpretaciones geométricas para captar la esencia del signo de la pendiente y su significado en el contexto de las representaciones gráficas de las ecuaciones lineales.
Relación entre la signo de la pendiente y los valores de los coeficientes a, b y c
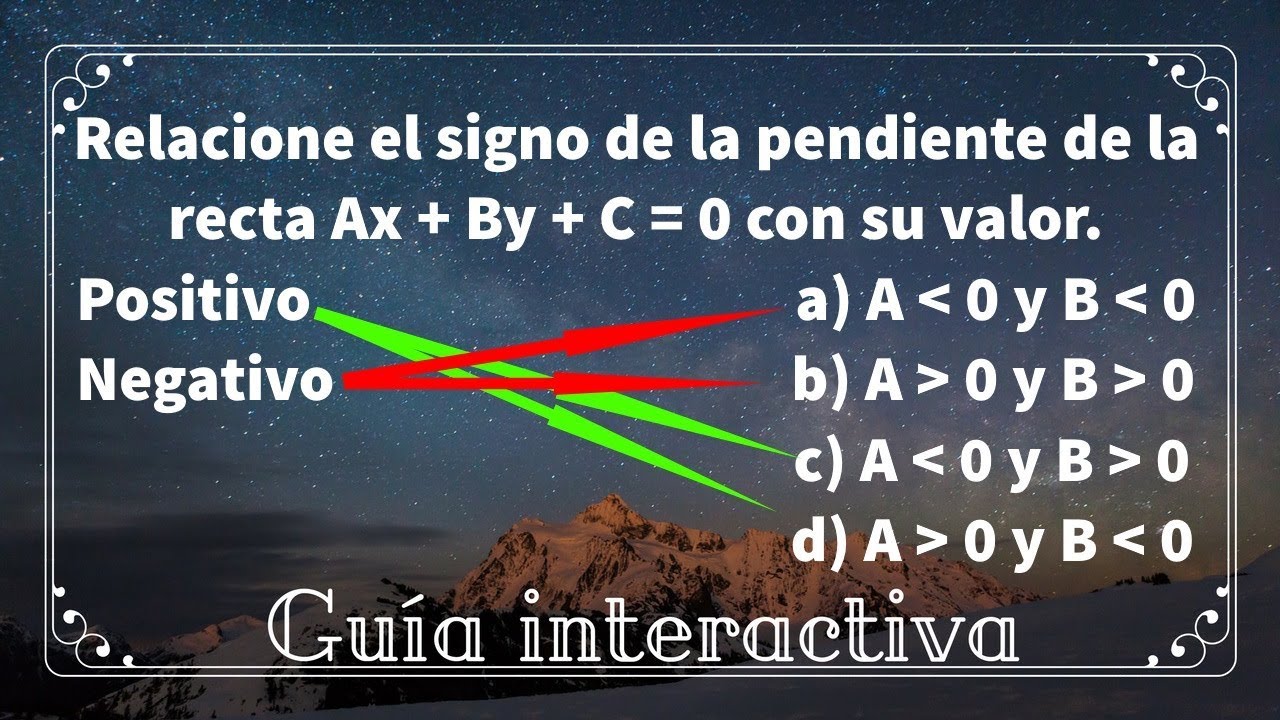
La relación entre el signo de la pendiente y los valores de los coeficientes a, b y c en la ecuación ax+by+c=0 es clave para comprender cómo las propiedades de la recta se ven afectadas por estos parámetros. Cuando se considera el signo de la pendiente, es crucial examinar las combinaciones de valores positivos y negativos de a y b en relación con el comportamiento de la recta en el plano.
Por ejemplo, si ‘a’ y ‘b’ son positivos, la pendiente será negativa, lo que indica una inclinación descendente. Del mismo modo, si ‘a’ es negativo y ‘b’ es positivo, la pendiente será positiva, lo que corresponde a una inclinación ascendente de la recta. Estas relaciones proporcionan información valiosa sobre la configuración de la recta y su dirección en el plano, estableciendo una conexión directa entre los signos de la pendiente y los coeficientes de la ecuación general.
Aplicaciones y ejemplos en el análisis de la pendiente de la recta
La comprensión del signo de la pendiente de la recta y su relación con los valores de los coeficientes a, b y c tiene una serie de aplicaciones en diversas áreas de las matemáticas y la física. Desde la interpretación de fenómenos físicos hasta la resolución de problemas de optimización en matemáticas, estos conceptos proporcionan herramientas fundamentales para el análisis y la modelización de situaciones del mundo real.
Un ejemplo concreto de aplicación es la interpretación de la pendiente en el contexto de la velocidad en física. Si consideramos una ecuación de movimiento en una dimensión, la pendiente de la recta resultante representa la velocidad instantánea del objeto en movimiento. El signo de la pendiente en este contexto puede indicar si el objeto se está moviendo en dirección positiva (hacia adelante) o negativa (hacia atrás), lo que tiene implicaciones significativas en la comprensión del comportamiento del sistema en cuestión.
Conclusiones y reflexiones finales
En conclusión, el signo de la pendiente de la recta en el contexto de la ecuación general ax+by+c=0 desempeña un papel fundamental en la comprensión y el análisis de las propiedades de las rectas en el plano cartesiano. La relación entre el signo de la pendiente y los valores de los coeficientes a, b y c proporciona una guía invaluable para interpretar el comportamiento geométrico y algebraico de las ecuaciones lineales, ofreciendo herramientas poderosas para el estudio de fenómenos variados.
Al considerar aplicaciones concretas en campos como la física y la ingeniería, se vuelve evidente cómo el análisis del signo de la pendiente puede arrojar luz sobre la naturaleza de diversos procesos y fenómenos, brindando una perspectiva enriquecedora para abordar problemas complejos y situaciones del mundo real. En última instancia, la comprensión detallada del signo de la pendiente enriquece nuestra capacidad para interpretar y modelar el comportamiento de sistemas y procesos en el ámbito matemático y científico.