Resolver ecuaciones lineales con términos constantes es un concepto fundamental en matemáticas. Este proceso permite encontrar el valor de la incógnita que satisface la igualdad entre dos expresiones lineales. A través de este artículo, exploraremos paso a paso cómo abordar y resolver este tipo de ecuaciones, desde su forma más básica hasta ejemplos más complejos.
Conociendo las ecuaciones lineales
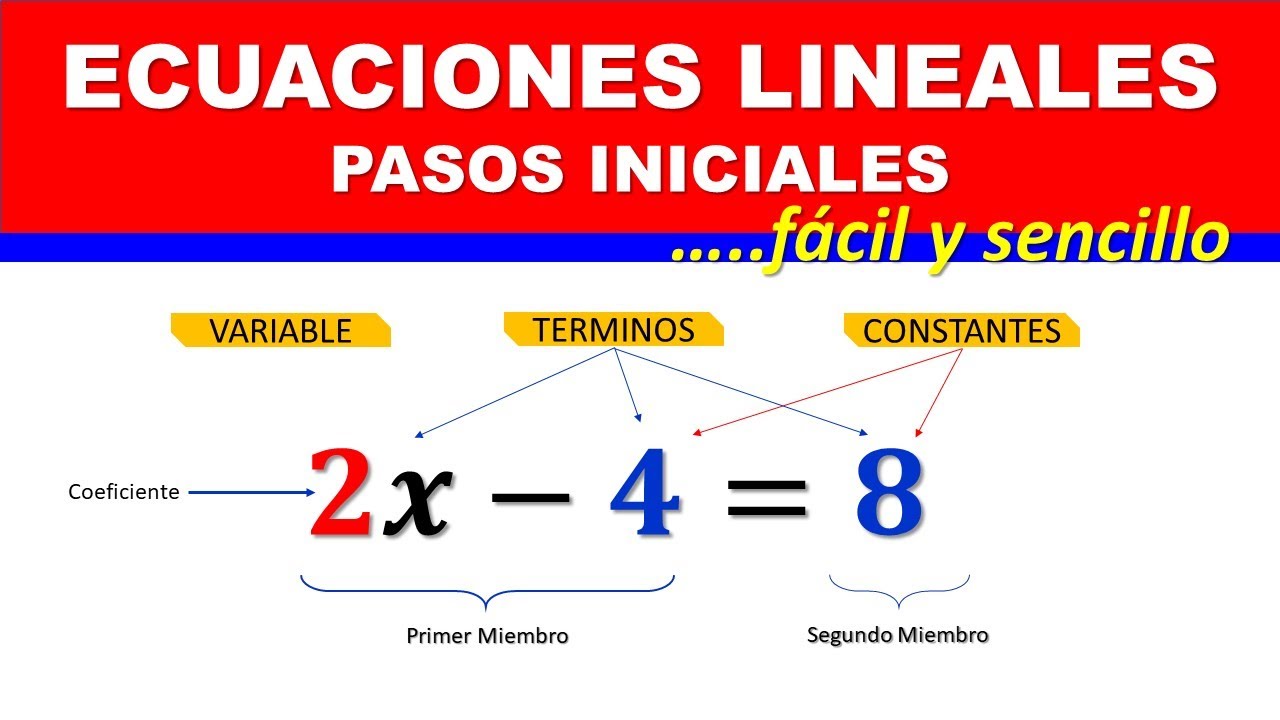
Antes de adentrarnos en la resolución de ecuaciones lineales con términos constantes, es crucial comprender la naturaleza de estas ecuaciones. Una ecuación lineal es una expresión matemática compuesta por variables y constantes, donde todas las operaciones involucradas son de primer grado. Por lo general, estas ecuaciones se representan en la forma ax + b = c, donde a, b y c son constantes, y x es la variable desconocida que buscamos hallar. Ahora que entendemos esto, estamos listos para abordar el proceso de solución.
Desglosando el proceso de solución
Para resolver una ecuación lineal con términos constantes, seguimos un conjunto de pasos claramente definidos que nos guiarán hacia la determinación del valor de la incógnita. Estos pasos incluyen la simplificación de la ecuación, el aislamiento de la variable, y la obtención del valor final. A continuación, detallaremos cada uno de estos pasos en profundidad y proporcionaremos ejemplos ilustrativos para una comprensión más clara.
Simplificación de la ecuación
El primer paso consiste en simplificar la ecuación, llevando a cabo las operaciones matemáticas necesarias para reducir términos semejantes y agrupar los términos con la incógnita en un solo lado de la igualdad. Este proceso nos permite trabajar con una expresión más manejable y nos acerca a la determinación del valor de la variable.
Aislamiento de la variable
Una vez simplificada la ecuación, el siguiente paso implica aislar la variable desconocida en un lado de la igualdad. Esto se logra aplicando operaciones inversas a las presentes en la ecuación, de modo que podamos despejar la variable y obtener su valor único. Es importante realizar estas operaciones de manera cuidadosa para evitar errores en el proceso.
Obtención del valor de la variable
Una vez que la variable ha sido aislada, llegamos al punto culminante del proceso: la obtención del valor numérico que satisface la ecuación. Al resolver la ecuación para la variable desconocida, llegamos a un resultado concreto que nos indica el valor exacto que hace que la igualdad sea válida. Este valor representa la solución de la ecuación y cumple con las condiciones establecidas inicialmente.
Ejemplos ilustrativos
Para solidificar nuestro entendimiento de la solución de ecuaciones lineales con términos constantes, consideremos algunos ejemplos prácticos que demuestren la aplicación de los pasos previamente discutidos. A través de estas ilustraciones, podremos ver en acción el proceso de resolución y comprender cómo se aplica en situaciones específicas.
Ejemplo 1: 3x + 5 = 11
Comencemos con una ecuación lineal sencilla. Para resolver esta ecuación, seguiremos los pasos establecidos. Primero, simplificaremos la ecuación restando 5 a ambos lados: 3x = 6. Luego, aislaremos la variable dividiendo por 3: x = 2. Finalmente, hemos obtenido el valor de la variable, lo que constituye la solución de la ecuación.
Ejemplo 2: 2y – 8 = 16
En este segundo ejemplo, nos enfrentamos a una ecuación con coeficientes diferentes. Aplicamos el proceso de resolución de manera similar: sumamos 8 a ambos lados para simplificar, obteniendo 2y = 24; luego, dividimos por 2 para aislar la variable, obteniendo y = 12. De esta forma, hemos encontrado el valor de la variable que cumple con la igualdad establecida.
La resolución de ecuaciones lineales con términos constantes es un proceso fundamental en matemáticas, con aplicaciones en numerosos contextos. A través de la comprensión detallada de los pasos involucrados y la práctica con ejemplos variados, podemos adquirir la destreza necesaria para abordar y resolver este tipo de ecuaciones de forma efectiva. A medida que avanzamos en nuestras habilidades matemáticas, la capacidad de resolver ecuaciones lineales se vuelve cada vez más crucial, lo que nos permite enfrentar desafíos más complejos con confianza y precisión.