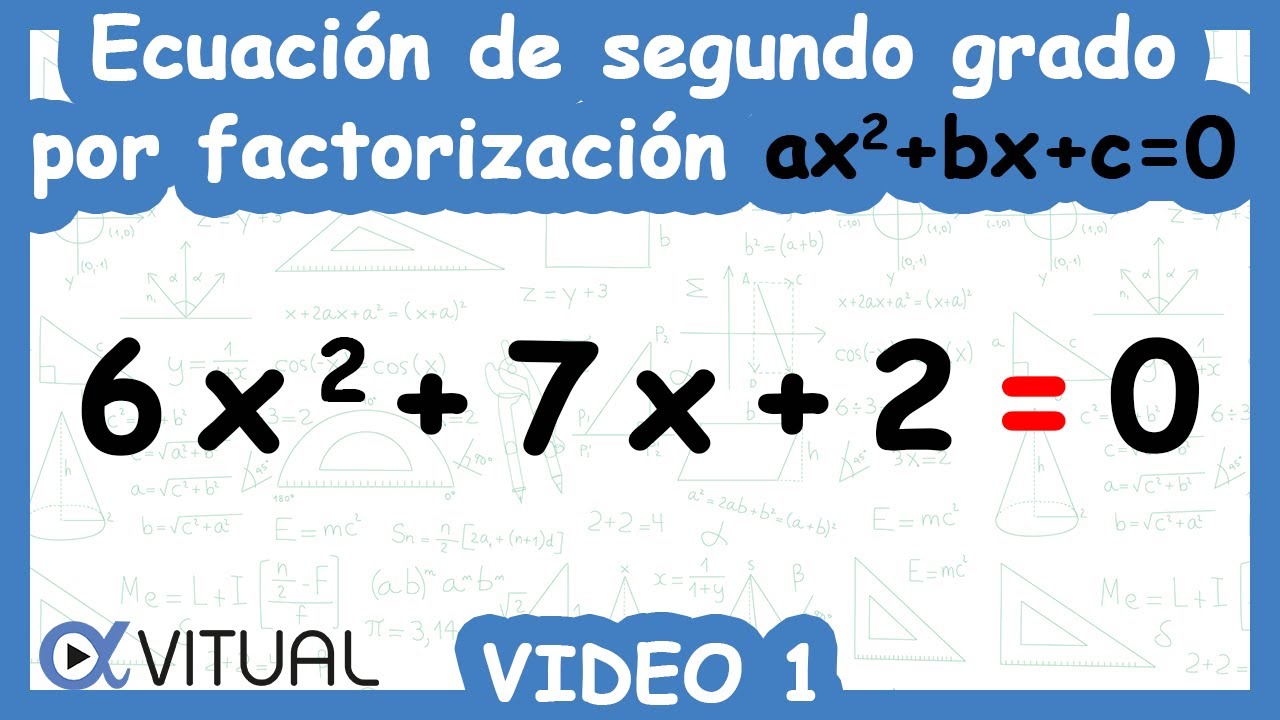
Solución de la ecuación cuadrática ax2 + bx + c = 0

Solución de la ecuación cuadrática ax2 + bx + c = 0

La ecuación cuadrática ax² + bx + c = 0 es una de las ecuaciones más importantes en la matemática, y su solución es de gran interés en campos como la física, la ingeniería y la economía.

Paso 1: Determinar los coeficientes a, b y c

Antes de comenzar a resolver la ecuación, es necesario determinar los valores de los coeficientes a, b y c. Estos coeficientes representan los diferentes términos presentes en la ecuación cuadrática y son necesarios para aplicar la fórmula general.

Paso 2: Aplicar la fórmula general

La fórmula general para resolver la ecuación cuadrática es:

x = (-b ± √(b² – 4ac)) / (2a)

Esta fórmula nos permite encontrar los valores de x que satisfacen la ecuación cuadrática.

Paso 3: Resolver la ecuación

1. Calcula el discriminante, que es el valor dentro de la raíz cuadrada en la fórmula general. El discriminante se calcula como b² – 4ac.
2. Si el discriminante es mayor que cero (> 0), la ecuación tiene dos soluciones reales y diferentes.
3. Si el discriminante es igual a cero (= 0), la ecuación tiene una solución real única.
4. Si el discriminante es menor que cero (< 0), la ecuación no tiene soluciones reales. En este caso, las soluciones son números complejos conjugados.

Una vez que se hayan determinado las soluciones, se pueden representar gráficamente en un plano cartesiano para visualizar mejor la ubicación de los puntos de intersección con el eje x.

En resumen, la solución de la ecuación cuadrática ax² + bx + c = 0 se obtiene aplicando la fórmula general y calculando el discriminante. Dependiendo del valor del discriminante, la ecuación tendrá dos soluciones reales y diferentes, una solución real única o dos soluciones complejas conjugadas.