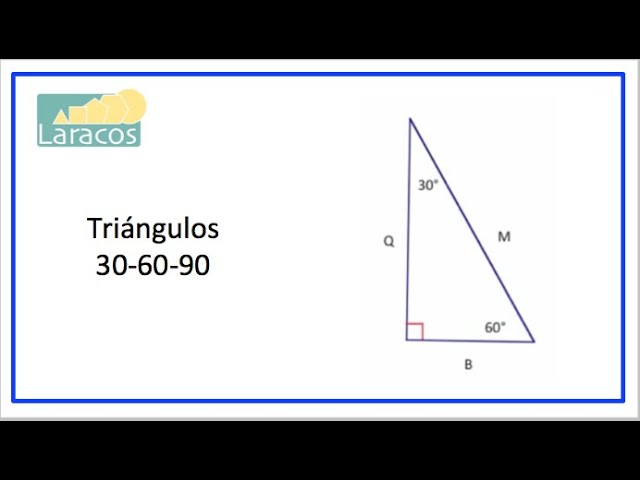
1. ¿Qué es un triángulo con ángulos de 90, 60 y 30 grados?
Un triángulo con ángulos de 90, 60 y 30 grados se conoce como un triángulo rectángulo.
En un triángulo rectángulo, uno de los ángulos es un ángulo recto, es decir, tiene 90 grados. En este tipo de triángulo, los otros dos ángulos son agudos, es decir, son menores a 90 grados.
El ángulo de 90 grados se llama ángulo recto, mientras que los ángulos de 60 grados y 30 grados se conocen como ángulos agudos. Estos ángulos agudos también son conocidos como ángulos complementarios, ya que su suma es igual a 90 grados.
2. Propiedades de un triángulo con ángulos de 90, 60 y 30 grados
Un triángulo con ángulos de 90, 60 y 30 grados tiene varias propiedades interesantes. Estas propiedades se derivan de las relaciones entre los ángulos y los lados del triángulo. Aquí hay algunas propiedades destacadas:
- Un triángulo con un ángulo de 90 grados se llama triángulo rectángulo. Este tipo de triángulo tiene un ángulo recto, que es un ángulo de 90 grados. En un triángulo rectángulo, el lado opuesto al ángulo recto se llama hipotenusa, y los otros dos lados se llaman catetos.
- La suma de los ángulos internos de un triángulo siempre es igual a 180 grados. Esto significa que si tenemos un ángulo de 90 grados, los otros dos ángulos deben sumar 90 grados para completar los 180 grados totales.
- En un triángulo rectángulo, el ángulo de 30 grados se encuentra junto al cateto más corto. Este ángulo se llama ángulo agudo porque mide menos de 90 grados. El cateto opuesto a este ángulo es la mitad de la longitud de la hipotenusa.
- La relación entre los lados de un triángulo rectángulo con ángulos de 30 y 60 grados sigue una proporción específica. Esta proporción se conoce como la razón trigonométrica del triángulo 30-60-90. Según esta proporción, el cateto opuesto al ángulo de 30 grados es la mitad de la longitud del cateto opuesto al ángulo de 60 grados. Además, la hipotenusa del triángulo es el doble de la longitud del cateto opuesto al ángulo de 30 grados.
Estas son solo algunas de las propiedades clave de un triángulo con ángulos de 90, 60 y 30 grados. Estudiar estas propiedades nos ayuda a comprender mejor las relaciones entre los ángulos y los lados de los triángulos rectángulos.
3. Fórmulas para calcular las longitudes de los lados del triángulo
En geometría, el triángulo es una figura compuesta por tres lados y tres ángulos. Calcular las longitudes de los lados de un triángulo es una tarea común al resolver problemas geométricos o al trabajar con teoremas y propiedades relacionadas con esta figura.
Existen diferentes fórmulas que nos permiten calcular la longitud de los lados de un triángulo, dependiendo de la información que tengamos del mismo. A continuación, presentaremos algunas de estas fórmulas:
Fórmula de la distancia:
Si conocemos las coordenadas de dos puntos A y B en un plano cartesiano, podemos calcular la distancia entre ellos utilizando la fórmula de la distancia. Esta fórmula se basa en el teorema de Pitágoras y se expresa de la siguiente manera:
d = √((x2 – x1)^2 + (y2 – y1)^2)
Donde (x1, y1) y (x2, y2) son las coordenadas de los puntos A y B respectivamente, y d es la distancia entre ellos.
Fórmula de Herón:
La fórmula de Herón es utilizada para calcular el área de un triángulo a partir de las longitudes de sus lados. Sin embargo, podemos usar esta fórmula para calcular la longitud de uno de los lados si conocemos el área y los otros dos lados. La fórmula se expresa de la siguiente manera:
a = 2A / (b + c)
Donde a es el lado que queremos calcular, A es el área del triángulo y b y c son los otros dos lados.
Teorema de Pitágoras:
El teorema de Pitágoras es ampliamente conocido y utilizado para calcular la longitud de uno de los lados de un triángulo rectángulo si conocemos las longitudes de los otros dos lados. La fórmula se expresa de la siguiente manera:
c = √(a^2 + b^2)
Donde c es la hipotenusa del triángulo (el lado opuesto al ángulo recto) y a y b son los otros dos lados.
Estas son solo algunas de las fórmulas que podemos utilizar para calcular las longitudes de los lados de un triángulo. Es importante tener en cuenta las condiciones y valores que conocemos del triángulo antes de aplicar una fórmula específica, para asegurar resultados precisos y válidos.
4. Ejemplos de triángulos con ángulos de 90, 60 y 30 grados
En geometría, los triángulos son una de las figuras más básicas y fundamentales. Un triángulo está compuesto por tres lados y tres ángulos. Dependiendo de la medida de sus ángulos, los triángulos pueden clasificarse en diferentes tipos.
Uno de los tipos más conocidos y estudiados es el triángulo rectángulo, aquel que tiene un ángulo recto de 90 grados. En este tipo de triángulo, los otros dos ángulos deben sumar 90 grados, por lo que son agudos. Uno de los ejemplos más comunes de triángulo rectángulo es el triángulo 3-4-5. Este triángulo tiene un ángulo de 90 grados, uno de 60 grados y otro de 30 grados.
Otro ejemplo de triángulo con ángulos de 90, 60 y 30 grados es el triángulo equilátero. Este tipo de triángulo tiene todos sus lados y ángulos iguales. En un triángulo equilátero, cada ángulo es de 60 grados, por lo que la suma de los tres ángulos se obtiene multiplicando ese valor por 3, lo que da como resultado los 180 grados que deben sumar todos los ángulos de un triángulo.
Algunos ejemplos de triángulos con ángulos de 90, 60 y 30 grados son:
- Triángulo rectángulo: Un triángulo con un ángulo recto de 90 grados y otros dos ángulos agudos de 60 y 30 grados.
- Triángulo equilátero: Un triángulo con tres ángulos iguales de 60 grados cada uno.
- Triángulo escalaeno: Un triángulo con tres ángulos diferentes, que pueden ser de 90, 60 y 30 grados.
Estos son solo algunos ejemplos de triángulos con ángulos de 90, 60 y 30 grados. Existen muchos más, cada uno con sus propias características y propiedades. La geometría es una rama fascinante de las matemáticas y los triángulos son uno de sus principales elementos de estudio.
5. Aplicaciones de los triángulos con ángulos de 90, 60 y 30 grados
Los triángulos con ángulos de 90, 60 y 30 grados, también conocidos como triángulos especiales, son extremadamente útiles en diversas aplicaciones prácticas.
1. Geometría y construcción
Estos triángulos se utilizan frecuentemente en geometría y construcción debido a sus propiedades bien definidas y fáciles de calcular. Su forma regular y sus ángulos específicos los hacen ideales para la creación de estructuras sólidas y estables.
2. Trigonometría
En trigonometría, los triángulos con ángulos de 90, 60 y 30 grados son ampliamente utilizados para calcular medidas de lados y ángulos en función de las ratios trigonométricas seno, coseno y tangente.
3. Física
Estos triángulos son especialmente relevantes en el campo de la física, donde se aplican en el estudio de la cinemática, la dinámica y la mecánica. Además, son utilizados para calcular fuerzas, velocidades y trayectorias en problemas relacionados con la resolución de triángulos rectángulos.
4. Matemáticas aplicadas
En matemáticas aplicadas, los triángulos con ángulos de 90, 60 y 30 grados son esenciales en campos como la ingeniería, la arquitectura y la navegación. Las propiedades y relaciones de estos triángulos permiten realizar cálculos precisos y determinar medidas desconocidas en muchos contextos prácticos.
5. Diseño gráfico y animación
En el diseño gráfico y la animación, los triángulos con ángulos de 90, 60 y 30 grados son utilizados para la creación de elementos visuales, como formas y efectos especiales. Su simplicidad y simetría atractiva los convierten en una opción popular para artistas y diseñadores.