¿Qué es un triángulo rectángulo?
Un triángulo rectángulo es un tipo de triángulo que tiene un ángulo recto, es decir, un ángulo de 90 grados. Su nombre proviene de la característica principal que lo distingue: la presencia de un ángulo recto. Este tipo de triángulo tiene muchas propiedades interesantes y útiles en matemáticas y geometría.
En un triángulo rectángulo, los lados que forman el ángulo recto se llaman catetos y el lado opuesto al ángulo recto se llama hipotenusa. Esta relación entre los catetos y la hipotenusa es esencial en el Teorema de Pitágoras, que establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
El Teorema de Pitágoras es una de las propiedades más fundamentales de los triángulos rectángulos y se utiliza ampliamente en cálculos matemáticos y aplicaciones prácticas. También permite calcular la longitud de un lado desconocido de un triángulo rectángulo cuando se conocen las longitudes de los otros dos lados.
En un triángulo rectángulo, los catetos y la hipotenusa establecen una relación especial con respecto a los ángulos. El seno, coseno y tangente son razones trigonométricas que se definen en función de los lados de un triángulo rectángulo. Estas relaciones trigonométricas se utilizan en campos como la navegación, la física y la ingeniería.
Las propiedades del triángulo rectángulo son útiles para resolver problemas de trigonometría y geometría en general. Además, los triángulos rectángulos se encuentran comúnmente en aplicaciones del mundo real, como en la construcción, en geometría de paisajes y en el diseño de estructuras.
En resumen, un triángulo rectángulo es un tipo de triángulo que tiene un ángulo recto. Sus características y propiedades, como el Teorema de Pitágoras y las relaciones trigonométricas, lo convierten en una figura geométrica muy importante en matemáticas y en diversas aplicaciones prácticas.
Propiedades del triángulo rectángulo
En geometría, el triángulo rectángulo es un tipo especial de triángulo que tiene un ángulo recto, es decir, un ángulo de 90 grados.
Algunas de las propiedades más importantes del triángulo rectángulo son:
1. Teorema de Pitágoras:
El famoso teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados. En forma de ecuación, podemos expresarlo de la siguiente manera:
c2 = a2 + b2
2. Relaciones trigonométricas:
En un triángulo rectángulo, se pueden establecer diversas relaciones trigonométricas entre los ángulos y las longitudes de sus lados. Algunas de las más conocidas son:
- Función seno: La longitud del cateto opuesto dividida por la hipotenusa.
- Función coseno: La longitud del cateto adyacente dividida por la hipotenusa.
- Función tangente: La longitud del cateto opuesto dividida por el cateto adyacente.
Estas relaciones son fundamentales en trigonometría y tienen aplicaciones en diversos campos como la navegación, la física y la geometría en general.
3. Congruencia:
Los triángulos rectángulos también pueden ser congruentes entre sí si tienen la misma longitud en sus lados y ángulos. Esto significa que si dos triángulos rectángulos tienen sus lados y ángulos iguales, entonces son congruentes y son considerados exactamente iguales.
En resumen, las propiedades del triángulo rectángulo incluyen el teorema de Pitágoras, las relaciones trigonométricas y la congruencia entre triángulos rectángulos.
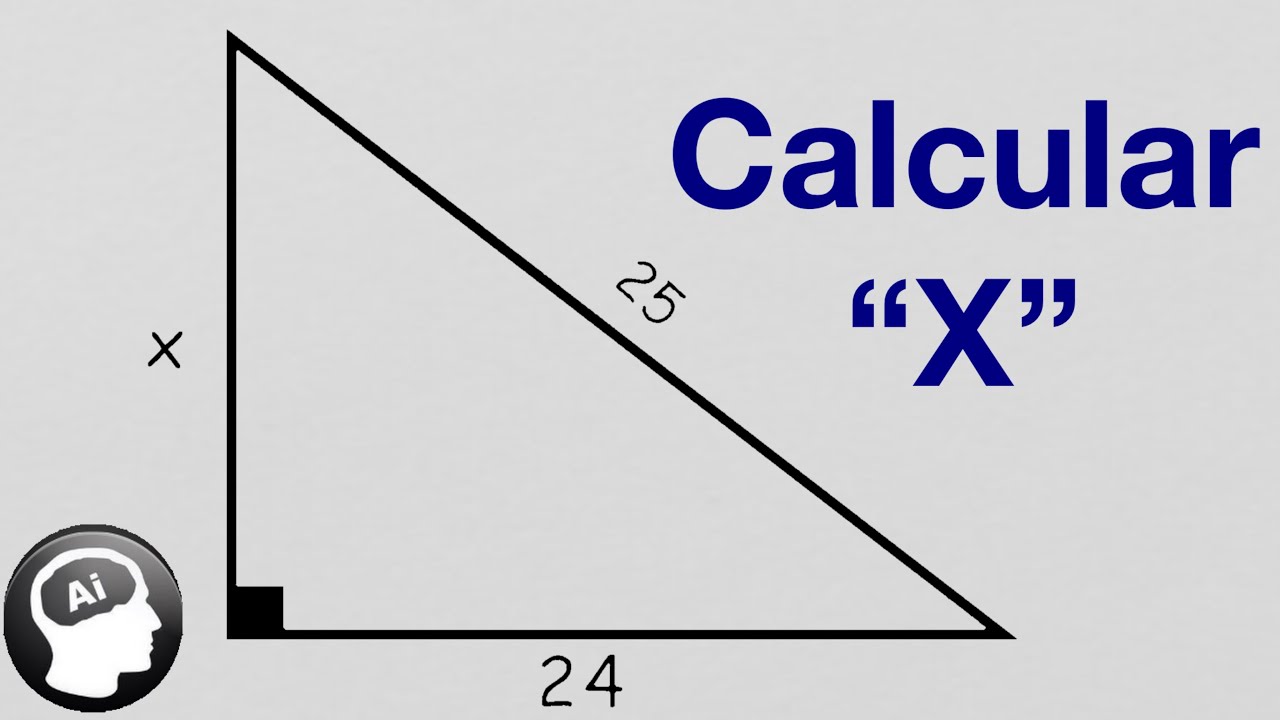
Cálculos en un triángulo rectángulo con hipotenusa de 25 cm
En un triángulo rectángulo, la hipotenusa es el lado más largo y se opone al ángulo recto. En este caso, tenemos un triángulo rectángulo con una hipotenusa de 25 cm.
Para realizar cálculos en este triángulo, podemos usar el teorema de Pitágoras, que establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados.
Si llamamos a los catetos a y b, podemos expresar esta relación matemáticamente como:
a^2 + b^2 = 25^2
Con esta ecuación, podemos calcular el valor de los catetos.
También podemos calcular la longitud de los lados restantes usando las razones trigonométricas. En un triángulo rectángulo, el coseno de un ángulo agudo es igual al cateto adyacente dividido por la hipotenusa, y el seno es igual al cateto opuesto dividido por la hipotenusa.
Por ejemplo, si queremos encontrar el valor del cateto adyacente al ángulo agudo X, podemos usar la siguiente ecuación:
cateto adyacente = hipotenusa * coseno(X)
De manera similar, si queremos encontrar el valor del cateto opuesto al ángulo agudo X, podemos usar la siguiente ecuación:
cateto opuesto = hipotenusa * seno(X)
Con estos cálculos, podemos determinar los valores de los catetos y los ángulos del triángulo rectángulo dado una hipotenusa de 25 cm.
Ejemplo práctico
En este ejemplo práctico vamos a utilizar diferentes etiquetas HTML para resaltar las frases más importantes del texto. Además, también añadiremos encabezados de nivel 3 (H3), listas y negritas () para darle más énfasis a ciertos elementos.
Etiqueta HTML <strong>
La etiqueta <strong> se utiliza para resaltar y hacer más fuerte el texto. Por ejemplo, en la siguiente frase: “El aprendizaje HTML es esencial para crear páginas web”, vamos a utilizar esta etiqueta para destacar la importancia del aprendizaje de HTML: El aprendizaje HTML es esencial para crear páginas web.
Encabezados de nivel 3 (H3)
Los encabezados de nivel 3 (H3) se utilizan para darle estructura y jerarquía al contenido de una página web. Por ejemplo, en el siguiente párrafo que habla sobre los beneficios de utilizar HTML, vamos a utilizar un encabezado de nivel 3 para resaltar esa sección:
Beneficios de utilizar HTML
- Facilidad de aprendizaje y uso.
- Compatibilidad con diferentes navegadores.
- Posibilidad de estructurar y dar formato al contenido.
Etiqueta HTML
La etiqueta se utiliza para aplicar negritas al texto. Por ejemplo, en la siguiente oración: “Es importante tener en cuenta las mejores prácticas al diseñar una página web”, utilizaremos la etiqueta para resaltar las mejores prácticas.
Con el uso de estas etiquetas y elementos, podemos resaltar visualmente las frases más importantes del texto, crear jerarquía en el contenido y enfatizar ciertos elementos mediante negritas.