Valor del lado AC de la figura aplicando el teorema de proporcionalidad

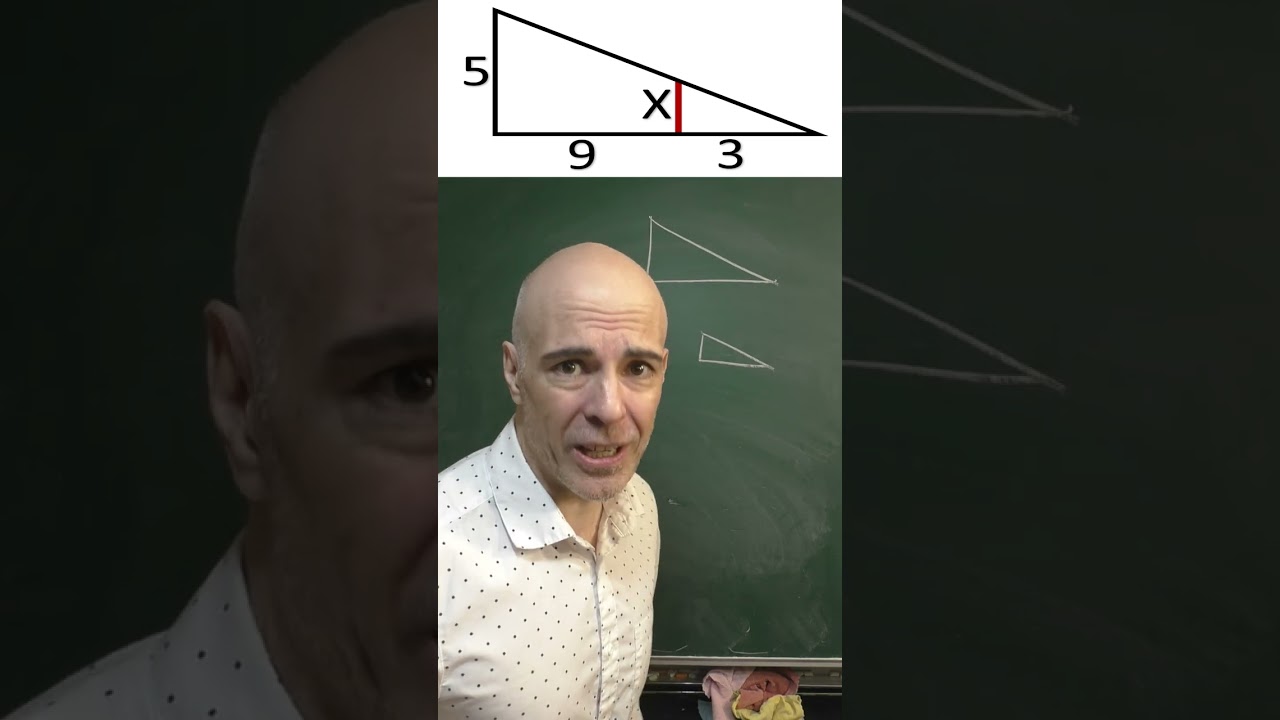
¿Qué es el teorema de proporcionalidad?

El teorema de proporcionalidad permite establecer una relación entre diferentes magnitudes, indicando si estas son proporcionales o no. En matemáticas, se considera que dos magnitudes son proporcionales si varían en la misma proporción o si se pueden expresar en forma de una fracción con una constante de proporcionalidad.

En otras palabras, si tenemos dos variables x e y, diremos que son proporcionales si siempre que x aumente o disminuya en una determinada cantidad, y también lo hará en la misma proporción.

Por ejemplo, si tenemos una relación de proporcionalidad entre el tiempo y la distancia recorrida por un vehículo a una velocidad constante, si duplicamos el tiempo, la distancia también se duplicará. Esto se puede expresar matemáticamente mediante la fórmula d = v * t, donde d es la distancia, v es la velocidad y t es el tiempo.

El teorema de proporcionalidad se puede expresar en forma de ecuación:

Si y = k * x, donde y es una variable dependiente, x es una variable independiente y k es una constante de proporcionalidad.

En ocasiones, el teorema de proporcionalidad se presenta de forma inversa. En este caso, se dice que dos magnitudes son inversamente proporcionales si al aumentar una de ellas, la otra disminuye en la misma proporción.

Existen diferentes métodos para determinar si dos magnitudes son proporcionales. Uno de ellos es a través de la construcción de una tabla de valores, donde se analiza si la relación entre las variables es constante. También se puede utilizar el método gráfico, trazando una recta que pase por los puntos correspondientes a los valores de las magnitudes.

En conclusión, el teorema de proporcionalidad es una herramienta fundamental en matemáticas para establecer la relación entre magnitudes y determinar si son proporcionales o no. Esta relación puede ser directa o inversa, y se puede expresar mediante fórmulas matemáticas o gráficamente.

Pasos para calcular el valor del lado AC aplicando el teorema de proporcionalidad

Paso 1: Obtener los valores de los lados conocidos

Antes de poder aplicar el teorema de proporcionalidad, es necesario conocer los valores de al menos dos lados del triángulo. Supongamos que conocemos los valores de los lados AB y BC.

• AB = 5 cm
• BC = 8 cm

Paso 2: Establecer una proporción entre los lados conocidos y el lado desconocido

El teorema de proporcionalidad establece que si dos triángulos son semejantes, entonces los lados correspondientes de los dos triángulos son proporcionales.

AB/BC = AC/CB

Paso 3: Despejar el valor del lado desconocido

Para calcular el valor del lado AC, podemos reordenar la ecuación de proporcionalidad de la siguiente manera:

AC = (AB * CB) / BC

Sustituyendo los valores conocidos:

AC = (5 cm * CB) / 8 cm

Paso 4: Resolver el cálculo

Si conocemos el valor de CB, podemos sustituirlo en la ecuación y resolver el cálculo para obtener el valor de AC.

Supongamos que CB = 10 cm:

AC = (5 cm * 10 cm) / 8 cm
AC = 50 cm / 8 cm
AC = 6.25 cm

Por lo tanto, el valor del lado AC es de 6.25 cm cuando AB = 5 cm y BC = 8 cm.

Ejemplo de cálculo del valor del lado AC

En este ejemplo vamos a calcular el valor del lado AC de un triángulo.

Para ello, necesitamos conocer la longitud de los otros dos lados del triángulo y el ángulo que se forma entre ellos.

Paso 1: Obtener los datos

Supongamos que conocemos la longitud del lado AB, que es de 8 unidades, y la longitud del lado BC, que es de 10 unidades.

También supongamos que el ángulo entre los lados AB y BC es de 45 grados.

Paso 2: Aplicar la ley de los cosenos

La ley de los cosenos nos permite calcular la longitud del lado AC utilizando la siguiente fórmula:

AC² = AB² + BC² – 2 * AB * BC * cos(ángulo)

En nuestro caso, esto se traduce en:

AC² = 8² + 10² – 2 * 8 * 10 * cos(45)

Paso 3: Calcular el valor de AC

Aplicando la fórmula, tenemos:

AC² = 64 + 100 – 160 * cos(45)

Como sabemos que cos(45) = 0.7071, podemos sustituirlo en la fórmula:

AC² = 64 + 100 – 160 * 0.7071

AC² = 64 + 100 – 113.1376

AC² ≈ 50.8624

Ahora, para obtener el valor de AC, calculamos la raíz cuadrada del resultado:

AC = √50.8624

Paso 4: Resultado final

Por lo tanto, el valor del lado AC es aproximadamente 7.13 unidades.

Este ha sido un ejemplo de cómo calcular el valor del lado AC de un triángulo utilizando la ley de los cosenos.

En este artículo hemos explorado diferentes formas de resaltar el texto en HTML utilizando etiquetas como , y encabezados de nivel 3 (

).

Al utilizar la etiqueta , pudimos hacer énfasis en las frases más importantes del texto, enfatizando su importancia. Esto también puede ayudar a los lectores a captar rápidamente la información clave.

También mencionamos la posibilidad de utilizar la etiqueta para aplicar el estilo de negrita al texto. Aunque es similar a la etiqueta , se recomienda utilizarla para resaltar palabras o frases de manera estilística, en lugar de indicar una importancia intrínseca.

Además, mencionamos cómo utilizar los encabezados de nivel 3 (

) para estructurar y organizar el contenido. Estos encabezados pueden ayudar a los lectores a navegar por el texto y encontrar fácilmente la información que están buscando.

En conclusión, al utilizar etiquetas HTML como , y los encabezados de nivel 3 (

), podemos resaltar y estructurar el texto de manera efectiva. Esto no solo mejora la legibilidad, sino que también proporciona una experiencia de lectura más agradable para los usuarios.