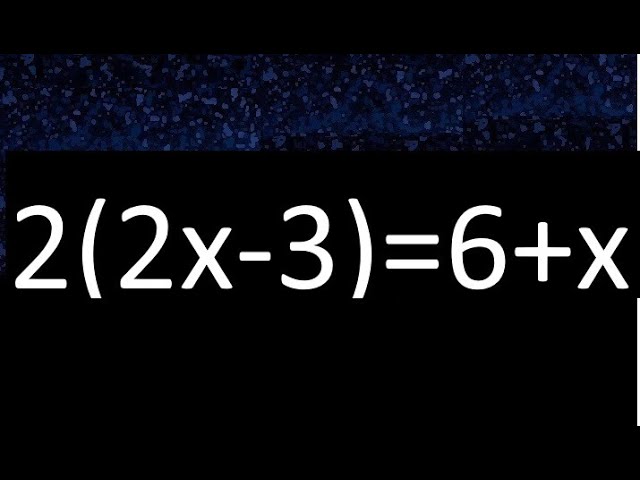Resolución de la ecuación 2(2x-3)=6x

¿Qué es una ecuación?

Una ecuación es una igualdad matemática que relaciona dos expresiones y se representa mediante un signo de igual (=). En una ecuación, las expresiones que se encuentran a cada lado del signo de igual son conocidas como miembros.

En la resolución de una ecuación, el objetivo es encontrar el valor o los valores de las incógnitas que satisfacen la igualdad establecida. Esto se logra aplicando diferentes operaciones matemáticas para despejar la incógnita y obtener su valor.

Tipos de ecuaciones

Existen diversos tipos de ecuaciones, cada una con características y métodos de resolución específicos. Algunos tipos comunes incluyen:

• Ecuaciones lineales: aquellas en las que solo aparecen variables de primer grado.
• Ecuaciones cuadráticas: aquellas en las que la variable está elevada al cuadrado.
• Ecuaciones exponenciales: aquellas en las que la variable se encuentra en el exponente de una potencia.
• Ecuaciones trigonométricas: aquellas que involucran funciones trigonométricas como el seno, coseno o tangente.

En la solución de ecuaciones, es importante asegurarse de buscar y considerar todas las posibles soluciones y verificar que estas cumplan con las restricciones establecidas en el problema.

En resumen, una ecuación es una igualdad matemática que relaciona dos expresiones y se utiliza para encontrar el valor o los valores de las incógnitas. Existen diferentes tipos de ecuaciones, cada una con métodos específicos de resolución.

Pasos para resolver la ecuación 2(2x-3)=6x

Para resolver la ecuación 2(2x-3)=6x, debemos seguir los siguientes pasos:

1. Paso 1: Distribuir el 2 en la expresión 2x-3, multiplicando cada término por 2.

Obtenemos: 4x – 6 = 6x

Anuncios
2. Paso 2: Restar 4x a ambos lados de la ecuación para agrupar los términos con x en un lado y los términos constantes en el otro lado.

Esto nos deja con: -6 = 2x

3. Paso 3: Dividir ambos lados de la ecuación por 2 para despejar x.
Quizás también te interese:  Cómo plantear una ecuación lineal con una variable en un contexto específico

Tenemos entonces: x = -6/2

4. Paso 4: Simplificar la fracción -6/2.

Obtenemos: x = -3

Por lo tanto, la solución de la ecuación 2(2x-3)=6x es x = -3.

1. Distribuir el 2 en la ecuación

Una de las operaciones básicas en matemáticas es la distribución, que nos permite simplificar una ecuación o expresión algebraica. En este caso, vamos a distribuir el número 2 en una ecuación para resolverla.

Supongamos que tenemos la siguiente ecuación: 3(x + 4) = 6(x - 2)

Para distribuir el 2 en la ecuación, multiplicamos el 2 por cada término dentro de los paréntesis. Esto resulta en:

3 * x + 3 * 4 = 6 * x - 6 * 2

Simplificamos los productos:

• 3x + 12 = 6x - 12

Ahora podemos reorganizar la ecuación para agrupar los términos variables en un lado y los términos constantes en el otro lado:

• 3x - 6x = -12 - 12
• -3x = -24

Dividimos ambos lados de la ecuación por -3 para despejar la variable:

• x = -24 / -3
• x = 8

Por lo tanto, la solución para la ecuación original es x = 8. Distribuir el 2 nos permitió simplificar la ecuación y encontrar el valor de la variable.

2. Reorganizar los términos

En esta sección, vamos a reorganizar los términos más importantes del texto utilizando etiquetas HTML para resaltarlos y darles mayor énfasis.

A continuación, presentaremos las frases destacadas utilizando las etiquetas <strong> </strong>:

1. El cambio climático es uno de los problemas más urgentes que enfrenta nuestro planeta.
2. La deforestación desempeña un papel importante en el calentamiento global.
3. La contaminación del aire está afectando la salud de las personas en todo el mundo.
4. El uso excesivo de plásticos está generando problemas ambientales a gran escala.

También podemos utilizar las etiquetas <b> </b> para resaltar algunas palabras o frases adicionales dentro de las frases destacadas:

1. El cambio climático es uno de los problemas más urgentes que enfrenta nuestro planeta.
2. La deforestación desempeña un papel importante en el calentamiento global.
3. La contaminación del aire está afectando la salud de las personas en todo el mundo.
4. El uso excesivo de plásticos está generando problemas ambientales a gran escala.

Además, podemos utilizar encabezados HTML, como el <h3>, para introducir secciones relacionadas con los términos destacados:

Cambio climático

El cambio climático es uno de los problemas más urgentes que enfrenta nuestro planeta. Es importante abordar este problema de manera colectiva para mitigar sus efectos.

Deforestación

La deforestación desempeña un papel importante en el calentamiento global. Es crucial tomar medidas para detener la pérdida de bosques y promover la reforestación.

Contaminación del aire

La contaminación del aire está afectando la salud de las personas en todo el mundo. Es necesario reducir las emisiones contaminantes y fomentar fuentes de energía más limpias.

Uso excesivo de plásticos

El uso excesivo de plásticos está generando problemas ambientales a gran escala. Debemos adoptar prácticas sostenibles y promover alternativas eco-amigables.

3. Simplificar la expresión

En matemáticas, simplificar una expresión es encontrar una forma más corta o más simple de escribirla sin cambiar el valor. Simplificar una expresión puede ser útil para resolver problemas o ecuaciones más fácilmente.

Para simplificar una expresión, es importante recordar algunas reglas básicas de operaciones matemáticas, como la propiedad conmutativa y distributiva, y las reglas de los exponentes.

Algunas estrategias comunes para simplificar expresiones incluyen:

• Combina términos semejantes: si tienes términos con variables iguales, puedes combinarlos sumando o restando sus coeficientes.
• Factoriza: busca factores comunes en los términos y factorízalos.
• Aplica las propiedades de los exponentes: simplifica las operaciones con exponentes, como multiplicar o dividir potencias con la misma base.
• Elimina paréntesis: utiliza la propiedad distributiva para eliminar paréntesis y simplificar la expresión.

Un ejemplo de cómo simplificar una expresión sería:

Expresión inicial: 3x + 2x – 5x + 7

Paso 1: Combina términos semejantes:

3x + 2x – 5x + 7 = (3 + 2 – 5)x + 7 = 0x + 7 = 7

La expresión simplificada es 7.

En resumen, simplificar una expresión implica aplicar reglas matemáticas para reducir su complejidad sin cambiar su valor. A través de estrategias como combinar términos semejantes, factorizar, aplicar las propiedades de los exponentes y eliminar paréntesis, podemos simplificar expresiones para facilitar su manipulación y resolución.

4. Despejar x

En álgebra, despejar la variable x es una habilidad fundamental que se utiliza para resolver ecuaciones y expresiones algebraicas. Cuando se despeja x, se busca encontrar el valor numérico de x que satisface la ecuación o expresión dada.

Para despejar x, se deben seguir una serie de pasos y propiedades matemáticas que permiten simplificar y transformar la ecuación hasta que x quede aislado en un lado de la igualdad. Veamos un ejemplo:

Supongamos que tenemos la ecuación 2x + 5 = 15. Para despejar x, seguimos los siguientes pasos:

1. Restamos 5 a ambos lados de la ecuación: 2x = 10
2. Dividimos ambos lados de la ecuación por 2: x = 5

De esta manera, hemos despejado x y hemos encontrado que x tiene un valor de 5 que satisface la ecuación dada.

Despejar x puede variar en complejidad según la ecuación o expresión dada. En algunos casos, puede requerir el uso de propiedades matemáticas avanzadas, como la resolución de ecuaciones cuadráticas. Sin embargo, la base para despejar x siempre se basa en manipular la ecuación de manera que se logre aislar la variable x.

Conclusión

Despejar la variable x en una ecuación es un proceso fundamental en el álgebra. Mediante la aplicación de propiedades matemáticas y pasos específicos, se puede simplificar y transformar una ecuación hasta que x quede aislado en un lado de la igualdad. Es una habilidad crucial para resolver problemas y trabajar con expresiones algebraicas.

5. Calcular el valor de x

En este problema, se nos pide calcular el valor de x. Para poder realizar este cálculo, necesitamos seguir los pasos adecuados y utilizar las fórmulas correspondientes.

Pasos para calcular x:

1. Identificar las ecuaciones o expresiones que contienen a x.
2. Simplificar las ecuaciones o expresiones, si es necesario.
3. Resolver las ecuaciones o expresiones para obtener el valor numérico de x.

Una vez que hemos identificado y simplificado las ecuaciones o expresiones relevantes, podemos proceder a resolverlas.

Ejemplo:

Supongamos que nos dan la ecuación siguiente:

2x + 5 = 15

En este caso, para calcular el valor de x, debemos aislar la variable. Restamos 5 a ambos lados de la ecuación:

2x = 10

A continuación, dividimos ambos lados de la ecuación por 2 para despejar x:

x = 5

Así, hemos encontrado que el valor de x que satisface la ecuación es 5.

Recuerda siempre verificar tus soluciones sustituyendo el valor encontrado en la ecuación original para confirmar que es correcto.

En conclusión, para calcular el valor de x, es importante seguir los pasos adecuados, identificar y simplificar las ecuaciones relevantes, y resolverlas utilizando las operaciones necesarias.