Funciones con exponentes como variable independiente

Funciones con exponentes como variable independiente

En matemáticas, una función con exponentes como variable independiente es aquella en la que el exponente de una variable específica determina el valor de la función. Este tipo de funciones es bastante común y se utiliza en diversos campos, como la física, la economía y las ciencias naturales.

Para comprender mejor este concepto, es importante tener en cuenta algunos elementos clave:

La base

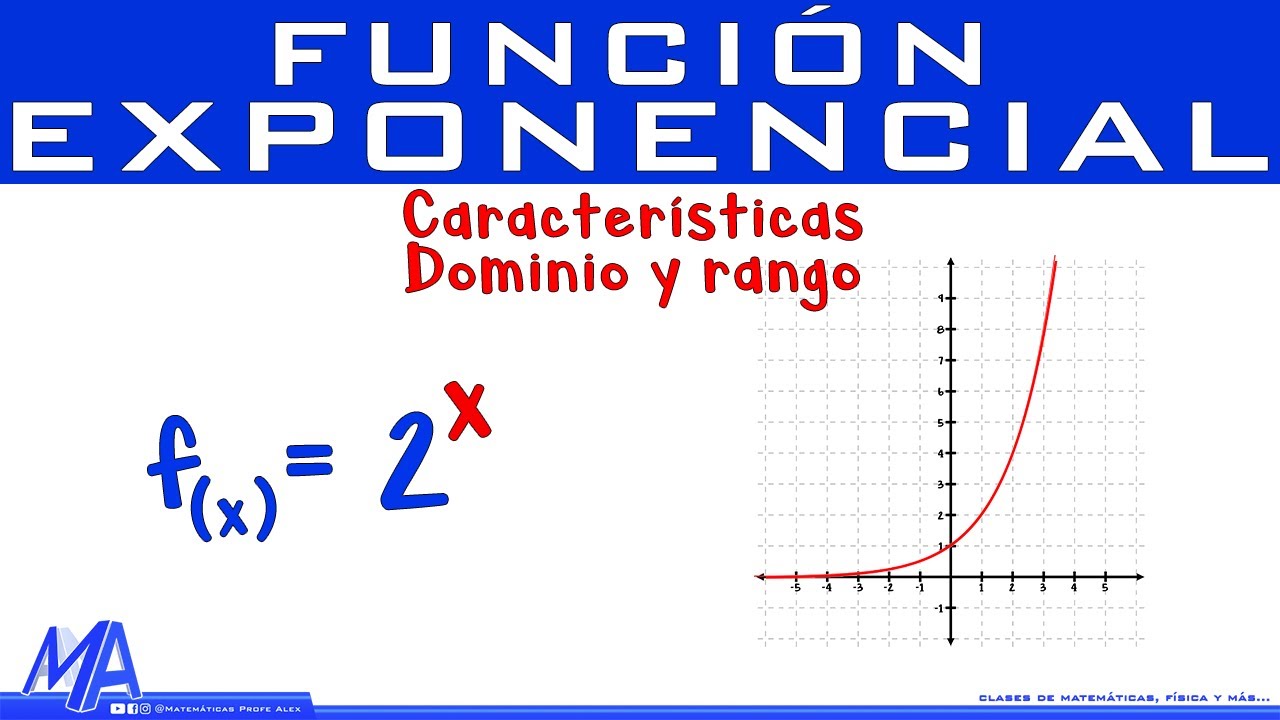
La base de una función con exponentes es el número que se eleva a una potencia. Por ejemplo, en la función f(x) = 2^x, el número 2 es la base.

El exponente

El exponente es un número que indica cuántas veces se debe multiplicar la base consigo misma. En el ejemplo anterior, el exponente es x.

Una de las propiedades más interesantes de las funciones con exponentes es que pueden representar tanto crecimiento como decrecimiento exponencial. Esto significa que, dependiendo del valor del exponente, la función puede crecer rápidamente hacia infinito o disminuir rápidamente hacia cero.

Por ejemplo, consideremos la función g(x) = 3^x. Si evaluamos algunos valores de x, obtendremos:

• g(0) = 3^0 = 1
• g(1) = 3^1 = 3
• g(2) = 3^2 = 9
• g(3) = 3^3 = 27

Podemos observar que a medida que x aumenta, el valor de la función se incrementa de manera exponencial.

Del mismo modo, si consideramos la función h(x) = (1/2)^x, y evaluamos algunos valores de x, obtendremos:

• h(0) = (1/2)^0 = 1
• h(1) = (1/2)^1 = 1/2
• h(2) = (1/2)^2 = 1/4
• h(3) = (1/2)^3 = 1/8

En este caso, a medida que x aumenta, el valor de la función disminuye de manera exponencial hacia cero.

Las funciones con exponentes también presentan propiedades interesantes cuando se combinan con otras funciones, como las funciones lineales o las funciones trigonométricas. Dependiendo del contexto y de las variables involucradas, pueden modelar fenómenos físicos, financieros o naturales de manera precisa.

En conclusión, las funciones con exponentes como variable independiente son una herramienta poderosa en matemáticas y en áreas científicas y económicas. Su capacidad para representar crecimiento o decrecimiento exponencial las convierte en un recurso invaluable para comprender mejor el mundo que nos rodea.

Cómo utilizar exponentes en funciones

Los exponentes son una herramienta fundamental en matemáticas y son ampliamente utilizados en funciones. Un exponente se utiliza para indicar la repetición de una cantidad. En funciones, los exponentes nos permiten elevar una variable a una potencia específica. Aquí te explicaré cómo utilizar exponentes en funciones.

1. Notación de exponente

En matemáticas, la notación de exponente se representa mediante el símbolo “^”. Por ejemplo, si tenemos la función f(x) = x^2, significa que la variable x se eleva al cuadrado. En este caso, el exponente es 2.

2. Ejemplos de funciones con exponentes

Veamos algunos ejemplos de funciones con exponentes:

• f(x) = x^3: Esta función eleva la variable x al cubo.
• g(x) = 2^x: En esta función, la base es 2 y el exponente es la variable x. Esto significa que la función nos da como resultado 2 elevado a la potencia x.
• h(x) = 10^(-x): Aquí, la base es 10 y el exponente es el negativo de la variable x. Esto nos indica que la función nos dará como resultado 10 elevado a la potencia negativa de x.

3. Propiedades de las funciones con exponentes

Las funciones con exponentes tienen varias propiedades importantes. Algunas de ellas son:

• El exponente cero: cualquier número elevado a la potencia cero es igual a 1. Por ejemplo, 2^0 = 1.
• La propiedad de la multiplicación: cuando tenemos una función f(x) = (a * b)^x, podemos distribuir el exponente a ambos términos de la multiplicación. Esto se traduce en f(x) = a^x * b^x.
• La propiedad de la división: si tenemos una función f(x) = a^x / b^x, podemos restar los exponentes de manera similar a la propiedad de la multiplicación. Esto se traduce en f(x) = (a/b)^x.

Estas propiedades nos permiten simplificar y manipular funciones con exponentes de manera más sencilla.

En resumen, utilizar exponentes en funciones nos permite expresar de manera más compacta y eficiente ciertos cálculos matemáticos. Con la notación adecuada y el conocimiento de las propiedades asociadas, podemos trabajar con funciones con exponentes de manera más efectiva.

Ejemplos de funciones con exponentes

Los exponentes son una herramienta matemática que se utiliza para representar multiplicaciones repetidas de un número por sí mismo. Las funciones con exponentes son expresiones matemáticas en las que se utiliza un exponente para indicar la repetición de una operación.

A continuación, se presentan algunos ejemplos de funciones con exponentes:

Ejemplo 1:

La función f(x) = 2^x es una función exponencial en la que el número 2 es la base y la variable x es el exponente. Al evaluar esta función para diferentes valores de x, obtenemos potencias de 2. Por ejemplo:

• f(0) = 2^0 = 1
• f(1) = 2^1 = 2
• f(2) = 2^2 = 4
• f(3) = 2^3 = 8

Ejemplo 2:

Otro ejemplo de función con exponente es la función g(x) = 3^x. En este caso, la base es 3 y la variable x es el exponente. Al evaluar esta función para diferentes valores de x, obtenemos potencias de 3. Por ejemplo:

• g(0) = 3^0 = 1
• g(1) = 3^1 = 3
• g(2) = 3^2 = 9
• g(3) = 3^3 = 27

Ejemplo 3:

También podemos tener funciones con exponentes negativos. Por ejemplo, la función h(x) = 5^(-x) tiene una base de 5 y el exponente es el valor negativo de x. Al evaluar esta función, obtenemos potencias inversas de 5. Por ejemplo:

• h(0) = 5^(-0) = 1
• h(1) = 5^(-1) = 1/5 = 0.2
• h(2) = 5^(-2) = 1/25 = 0.04
• h(3) = 5^(-3) = 1/125 = 0.008

Estos son solo algunos ejemplos de funciones con exponentes. Las funciones exponenciales son muy útiles en diversas áreas de la matemática y las ciencias, ya que nos permiten modelar crecimientos y decaimientos exponenciales.

Propiedades de las funciones con exponentes

Las funciones con exponentes son una parte fundamental de la matemática y tienen propiedades importantes que debemos comprender. A continuación, presentaremos algunas de estas propiedades:

1. Propiedad de la adición: Si tenemos dos funciones con exponentes iguales, podemos sumar o restar los exponentes manteniendo la misma base. Por ejemplo, 2^3 + 2^3 = 2^(3+3) = 2^6.
2. Propiedad de la multiplicación: Cuando multiplicamos dos funciones con exponentes con la misma base, podemos sumar los exponentes. Por ejemplo, (2^3) x (2^4) = 2^(3+4) = 2^7.
3. Propiedad de la división: Si dividimos dos funciones con exponentes con la misma base, podemos restar los exponentes. Por ejemplo, (2^5) / (2^2) = 2^(5-2) = 2^3.
4. Propiedad de la potencia de una potencia: Si una función con exponente está elevada a otra potencia, podemos multiplicar los exponentes. Por ejemplo, (2^3)^2 = 2^(3×2) = 2^6.
5. Propiedad de la raíz: Si tenemos una raíz de una función con exponente, podemos dividir el exponente por el índice de la raíz. Por ejemplo, √(2^4) = 2^(4/2) = 2^2.

Estas propiedades son fundamentales para simplificar y resolver ecuaciones con funciones con exponentes. Es importante recordarlas y aplicarlas correctamente para obtener resultados precisos en nuestros cálculos. ¡Practiquemos y exploremos el maravilloso mundo de las funciones con exponentes!

Aplicaciones prácticas de las funciones con exponentes

Las funciones con exponentes son una herramienta matemática versátil y poderosa que se utiliza en una variedad de aplicaciones prácticas en diferentes campos.

Una de las aplicaciones más comunes de las funciones con exponentes es en la modelización de crecimiento y decaimiento. Por ejemplo, en la biología, se pueden utilizar funciones exponenciales para describir el crecimiento de una población a lo largo del tiempo. Esto es especialmente útil en el estudio de enfermedades, donde se puede predecir la propagación de una enfermedad en una población a través de modelos matemáticos basados en funciones exponenciales.

En física, las funciones con exponentes también se utilizan para describir fenómenos como el decaimiento radiactivo. Los núcleos radiactivos tienen una tasa constante de decaimiento a lo largo del tiempo, lo que se puede modelar utilizando una función exponencial.

En economía, las funciones con exponentes son ampliamente utilizadas para el cálculo de intereses compuestos. En este caso, la función exponencial representa el crecimiento de una inversión a lo largo del tiempo, teniendo en cuenta el interés que se acumula periódicamente.

Además, las funciones con exponentes también tienen aplicaciones en la teoría de probabilidad. Por ejemplo, en el cálculo de probabilidades de eventos independientes y sucesivos, se utilizan funciones exponenciales para determinar la probabilidad de que ocurra un evento en un intervalo de tiempo específico.

En resumen, las funciones con exponentes tienen numerosas aplicaciones prácticas en diversos campos como la biología, la física, la economía y la teoría de probabilidad. Su capacidad para modelar el crecimiento y el decaimiento, así como el cálculo de intereses compuestos y probabilidades, las convierten en una herramienta matemática fundamental.