El plano cartesiano es una herramienta matemática fundamental utilizada para representar puntos en un espacio bidimensional. Fue creado por René Descartes y es ampliamente utilizado en diversos campos, como la geometría, la trigonometría, la física y la ingeniería. Comprender los elementos del plano cartesiano es esencial para el estudio y la aplicación de conceptos matemáticos y científicos.
Los componentes del plano cartesiano
Los elementos básicos del plano cartesiano incluyen dos ejes, el eje x y el eje y, que se intersectan en el origen. El eje x representa la coordenada horizontal, mientras que el eje y representa la coordenada vertical. Estos ejes dividen el plano en cuatro cuadrantes, numerados en sentido antihorario a partir del primer cuadrante en la esquina superior derecha.
El eje x y el eje y
El eje x se extiende de manera horizontal a lo largo del plano, con valores positivos a la derecha del origen y valores negativos a la izquierda. El eje y se extiende verticalmente, con valores positivos por encima del origen y valores negativos por debajo.
El origen
El origen, marcado como el punto (0,0), es el punto de intersección de los ejes x e y. Todas las coordenadas en el plano cartesiano se calculan con referencia a este punto.
Representación de puntos en el plano cartesiano
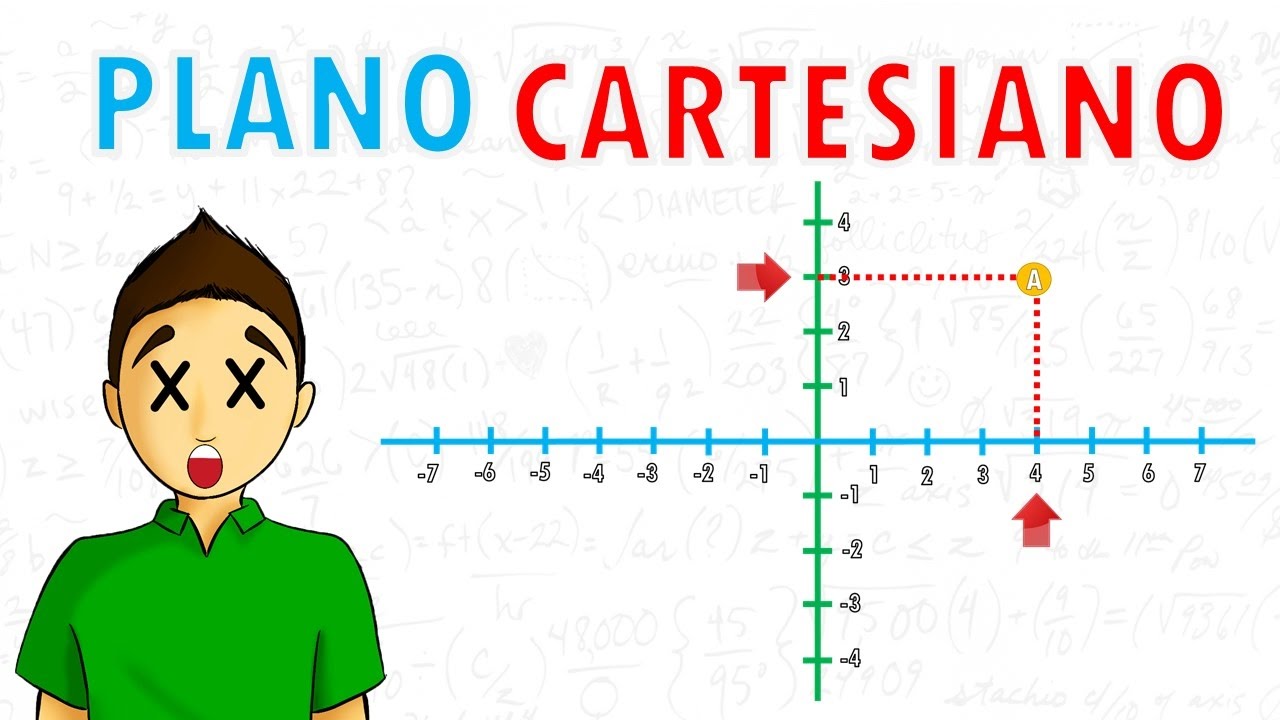
Los puntos en el plano cartesiano se representan por pares ordenados de números, donde el primer número representa la coordenada x y el segundo número representa la coordenada y. Por ejemplo, el punto (3,5) se encuentra a tres unidades a la derecha del origen y cinco unidades por encima del origen.
Ubicación de los puntos en los cuadrantes
Los cuadrantes del plano cartesiano permiten determinar la ubicación de un punto según el signo de sus coordenadas. Por ejemplo, si un punto tiene coordenadas (2,3), estará ubicado en el primer cuadrante, ya que ambas coordenadas son positivas.
Distancia entre dos puntos
La distancia entre dos puntos en el plano cartesiano se puede calcular utilizando la fórmula de distancia entre dos puntos, que se deriva del teorema de Pitágoras. Esta fórmula es fundamental para la geometría analítica y la resolución de problemas en el plano cartesiano.
Ecuaciones lineales y rectas en el plano cartesiano
Las ecuaciones lineales y rectas son representaciones fundamentales en el plano cartesiano. Una ecuación lineal tiene la forma y = mx + b, donde m representa la pendiente de la recta y b representa el término independiente. La pendiente indica la inclinación de la recta, mientras que el término independiente indica el punto en el que la recta corta el eje y. La representación gráfica de una ecuación lineal es una recta en el plano cartesiano.
Intersección de rectas
La intersección de dos rectas en el plano cartesiano se produce cuando comparten un punto común. Este punto de intersección es la solución del sistema de ecuaciones formado por las dos rectas. Comprender la intersección de rectas es esencial para resolver problemas de geometría analítica y sistemas de ecuaciones lineales.
Áreas y figuras geométricas en el plano cartesiano
El plano cartesiano también se utiliza para representar figuras geométricas, como triángulos, cuadrados, círculos y elipses. Las coordenadas de los vértices de la figura permiten trazarla en el plano cartesiano y calcular propiedades como área, perímetro y ecuaciones específicas que describen la figura.
Coordenadas de los vértices
Al asignar coordenadas a los vértices de una figura geométrica, es posible determinar su forma, tamaño y posición en el plano cartesiano. Esta representación facilita el cálculo de propiedades geométricas como área y perímetro.
Aplicaciones del plano cartesiano en la vida cotidiana
El plano cartesiano tiene numerosas aplicaciones en la vida cotidiana, desde la navegación utilizando coordenadas geográficas hasta el diseño de objetos en ingeniería y arquitectura. La comprensión de los elementos del plano cartesiano es fundamental para el desarrollo de habilidades en matemáticas y ciencias.
La navegación utilizando coordenadas geográficas, como la latitud y longitud, se basa en el concepto del plano cartesiano. Este sistema permite ubicar puntos específicos en la superficie terrestre y trazar rutas con precisión.
Diseño y geometría en la arquitectura
En el campo de la arquitectura, el plano cartesiano se utiliza para representar planos, elevaciones y diseños tridimensionales de edificios. Las coordenadas espaciales son esenciales para la planificación y construcción de estructuras arquitectónicas.
Aplicación en la ingeniería y la física
En ingeniería y física, el plano cartesiano se utiliza para modelar y resolver problemas relacionados con fuerzas, movimientos y sistemas de coordenadas. La representación gráfica de datos y ecuaciones permite visualizar y analizar fenómenos físicos de manera efectiva.