La probabilidad es una parte fundamental de las matemáticas y desempeña un papel crucial en una amplia gama de aplicaciones en la vida cotidiana y en campos tan diversos como la ingeniería, la economía y la ciencia de datos. En el contexto de las variables aleatorias continuas, los cálculos de probabilidad adquieren una complejidad adicional, ya que estas variables pueden tomar un número infinito de posibles valores dentro de un intervalo.
Definición de variable aleatoria continua
Una variable aleatoria continua es aquella cuyos valores posibles forman un intervalo no numerable. En otras palabras, la variable puede tomar cualquier valor dentro de un rango especificado, en contraste con las variables aleatorias discretas, que solo pueden tomar valores distintos y a menudo finitos. Ejemplos comunes de variables aleatorias continuas incluyen el tiempo de espera en una fila, la temperatura medida en grados Celsius, y la altura de un grupo de personas.
Distribución de probabilidad en variables aleatorias continuas
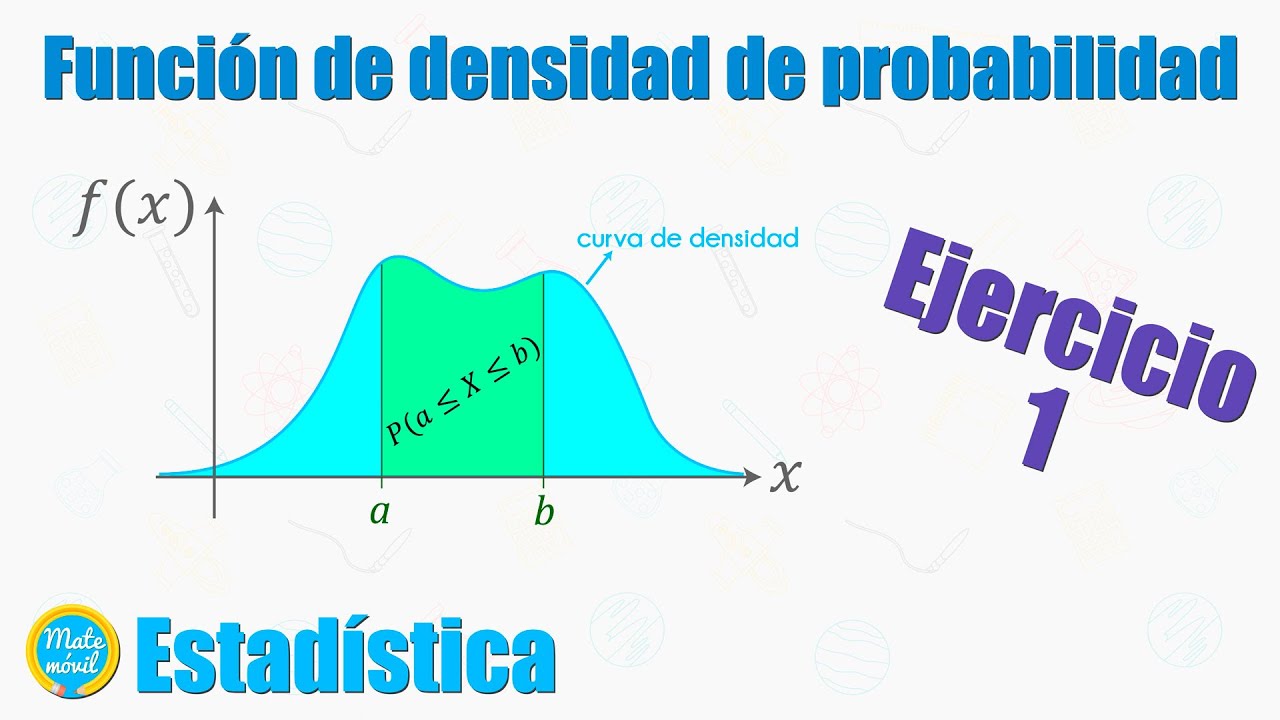
La función de densidad de probabilidad (PDF) es fundamental para comprender la distribución de probabilidad en variables aleatorias continuas. Mientras que en el caso de variables aleatorias discretas utilizamos la función de masa de probabilidad (PMF), en el caso continuo trabajamos con la PDF. La PDF es una función no negativa que integra a 1 sobre todo el rango de valores posibles de la variable aleatoria.
Densidad de probabilidad y probabilidad acumulativa
La densidad de probabilidad describe cómo están distribuidas las probabilidades a lo largo del rango de valores posibles de la variable aleatoria. Por otro lado, la probabilidad acumulativa nos proporciona la probabilidad de que la variable aleatoria sea menor o igual a un valor específico. Estas dos funciones son fundamentales para calcular la probabilidad en el contexto de las variables aleatorias continuas.
Función de distribución acumulativa
La función de distribución acumulativa (CDF) nos brinda la probabilidad de que una variable aleatoria continua sea menor o igual a un valor específico. Esta función es crucial para realizar cálculos de probabilidad en contextos prácticos, ya que nos permite evaluar probabilidades acumulativas de manera eficiente.
Cálculos de probabilidades con variables aleatorias continuas
Resolver problemas que involucran variables aleatorias continuas requiere el uso de integrales para calcular áreas bajo la curva de la PDF. Esta técnica es fundamental para determinar la probabilidad de que una variable aleatoria caiga en un cierto intervalo o para calcular valores esperados y varianzas en este contexto.
Calculando probabilidades específicas
Una vez que tenemos la función de densidad de probabilidad, podemos utilizarla para calcular probabilidades específicas asociadas con la variable aleatoria continua. Esto implica evaluar la integral de la PDF sobre un intervalo particular de valores, lo que nos proporciona la probabilidad de que la variable aleatoria esté dentro de ese rango.
Valor esperado y varianza en variables aleatorias continuas
El valor esperado de una variable aleatoria, denotado por E(X), es la media ponderada de todos los posibles valores que puede tomar la variable, donde el peso para cada valor es dado por la PDF. La varianza, por otro lado, mide qué tan dispersos están los valores alrededor del valor esperado. Calcular el valor esperado y la varianza en el contexto de variables aleatorias continuas implica el uso de integrales para realizar sumas ponderadas y cálculos de potencias.
Distribuciones de probabilidad comunes para variables aleatorias continuas
Existen varias distribuciones de probabilidad que son comúnmente utilizadas en el contexto de variables aleatorias continuas, cada una con sus propias características distintivas y aplicaciones en diversos campos.
Distribución normal
La distribución normal, también conocida como distribución gaussiana, es una de las más importantes y ampliamente utilizadas en estadística y probabilidad. Su característica en forma de campana la hace adecuada para modelar una amplia gama de fenómenos naturales y sociales. La función de densidad de probabilidad de la distribución normal es simétrica alrededor de su media y está completamente determinada por su media y desviación estándar.
Distribución exponencial
La distribución exponencial es particularmente útil para modelar el tiempo entre eventos en un proceso de conteo, ya que captura la probabilidad de que ocurra un evento en un intervalo de tiempo específico. Es comúnmente utilizada en problemas de fiabilidad, teoría de colas y en el análisis de supervivencia.
Distribución uniforme
La distribución uniforme es simple pero fundamental, ya que modela una situación en la que todas las observaciones en un intervalo tienen la misma probabilidad de ocurrir. Es comúnmente utilizada en el muestreo aleatorio y en la generación de números aleatorios en simulaciones computacionales.
Aplicaciones en la vida real
El cálculo de probabilidades en el contexto de variables aleatorias continuas tiene numerosas aplicaciones en una variedad de campos, desde la ingeniería y la física hasta la economía y las ciencias de la vida.
Ingeniería y ciencias físicas
En la ingeniería y las ciencias físicas, el análisis de sistemas dinámicos y el modelado de fenómenos naturales requieren el uso extensivo de cálculos de probabilidad en variables aleatorias continuas. Estas herramientas son fundamentales para comprender la incertidumbre asociada con mediciones y fenómenos físicos.
Finanzas y economía
En finanzas y economía, el cálculo de probabilidades en variables aleatorias continuas es crucial para modelar el precio de activos financieros, evaluar el riesgo y comprender la dinámica de los mercados. La distribución normal, en particular, es ampliamente utilizada en el modelado financiero debido a su capacidad para capturar la variabilidad de los rendimientos de activos.
Ciencias de la vida y medicina
En las ciencias de la vida y la medicina, el análisis de datos biológicos y médicos a menudo involucra variables aleatorias continuas, como la distribución del tiempo entre eventos biológicos o la distribución de tamaños de poblaciones. El uso de cálculos de probabilidad en este contexto es esencial para comprender la variabilidad en los datos y tomar decisiones informadas.
Los cálculos de probabilidad en variables aleatorias continuas son fundamentales para comprender la incertidumbre y la variabilidad en una amplia gama de aplicaciones. Desde el modelado de fenómenos naturales hasta la toma de decisiones en contextos financieros y médicos, la comprensión de la probabilidad en variables aleatorias continuas es esencial para la resolución de problemas en el mundo real.