Definición de un lugar geométrico
Un lugar geométrico es un conjunto de puntos que cumplen una cierta condición o propiedad. Para entender mejor este concepto, vamos a analizarlo paso a paso:
1. Puntos
En geometría, un punto se representa como una posición en el espacio, sin dimensiones ni tamaño. Es simplemente una ubicación. Por ejemplo, el punto A.
2. Condición o propiedad
La condición o propiedad establece las características que deben cumplir los puntos para pertenecer al lugar geométrico. Por ejemplo, “todos los puntos que están a la misma distancia de un punto fijo llamado centro forman una circunferencia”. En este caso, la condición es que los puntos estén a la misma distancia del centro.
3. Conjunto de puntos
El lugar geométrico es el conjunto de todos los puntos que cumplen la condición o propiedad establecida. Este conjunto puede ser definido de diferentes maneras, como una línea recta, una circunferencia, un plano, etc. Por ejemplo, la circunferencia es el lugar geométrico de todos los puntos que están a la misma distancia del centro.
En resumen, un lugar geométrico es un conjunto de puntos que cumplen una cierta condición o propiedad. Es una herramienta fundamental en geometría para representar y analizar formas y figuras.
Propiedades de un lugar geométrico con pendiente constante
Un lugar geométrico con pendiente constante tiene algunas propiedades importantes que lo definen y lo diferencian de otros lugares geométricos. Estas propiedades son fundamentales para comprender y trabajar con este tipo de lugares geométricos.
Pendiente constante
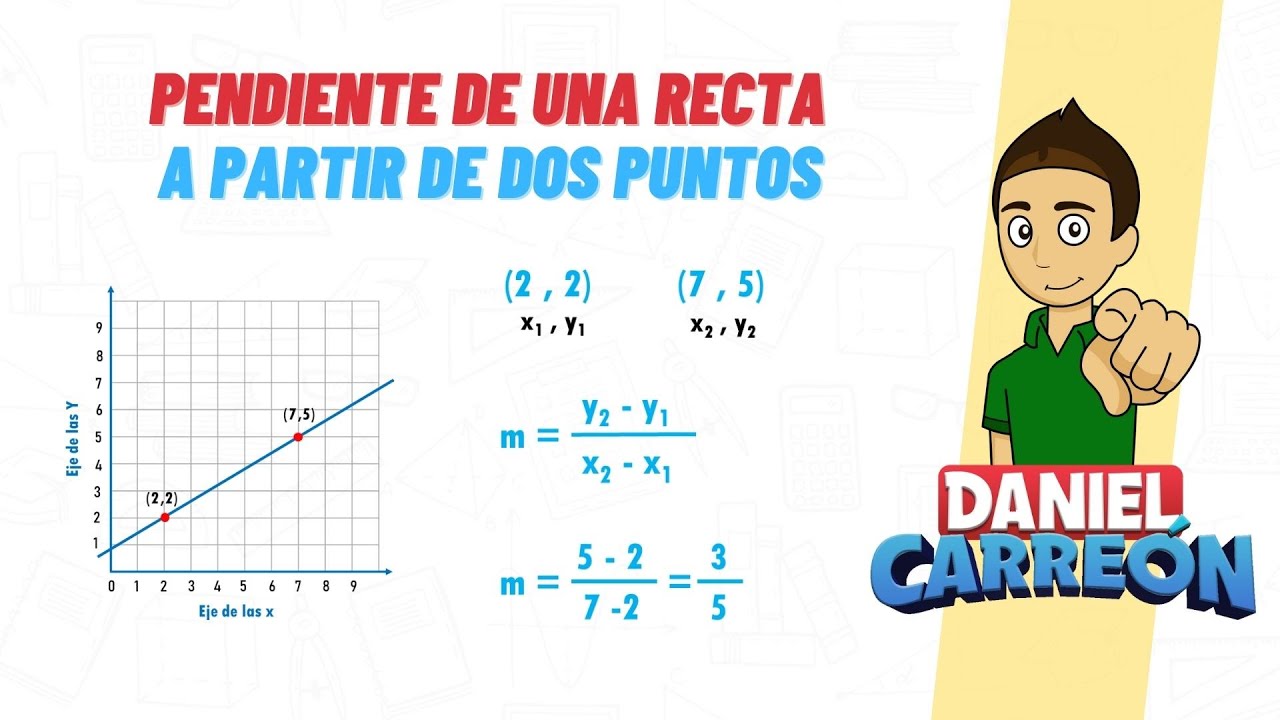
La principal propiedad de un lugar geométrico con pendiente constante es que todas sus rectas tienen la misma pendiente. Esto significa que si tomamos cualquier par de puntos en el lugar geométrico y trazamos una recta que los conecte, la pendiente de esa recta será siempre la misma.
Rectas paralelas
Otra propiedad importante de un lugar geométrico con pendiente constante es que todas sus rectas son paralelas entre sí. Esto se debe a que la pendiente determina la inclinación de las rectas, y al ser constante, todas las rectas tendrán esa misma inclinación y, por lo tanto, serán paralelas entre sí.
Intersección con los ejes
Un lugar geométrico con pendiente constante siempre intersecta los ejes de coordenadas en puntos diferentes. La recta que representa el lugar geométrico tiene una pendiente constante, lo que implica que nunca será horizontal ni vertical, por lo tanto, siempre cortará a los ejes en puntos distintos.
Relación con la ecuación de la recta
Un lugar geométrico con pendiente constante puede ser representado mediante una ecuación de la recta en su forma general. Esta ecuación tiene la forma y = mx + b, donde m representa la pendiente constante y b es el término independiente que determina la intersección con el eje y.
En conclusión, un lugar geométrico con pendiente constante se caracteriza por tener todas sus rectas con la misma pendiente, rectas paralelas entre sí, intersecciones diferentes con los ejes y una ecuación de la recta que lo describe. Estas propiedades son esenciales para comprender y trabajar con este tipo de lugares geométricos.
Ejemplos de lugares geométricos con pendiente constante
En geometría, un lugar geométrico se define como el conjunto de todos los puntos que cumplen una determinada condición. La pendiente es una medida de la inclinación de una recta y se representa con la letra m.
1. Recta
La recta es el lugar geométrico más básico con una pendiente constante. La pendiente determina la inclinación de la recta y puede ser positiva, negativa o cero. Si la pendiente es positiva, la recta sube de izquierda a derecha. Si la pendiente es negativa, la recta baja de izquierda a derecha. Si la pendiente es cero, la recta es horizontal.
2. Circunferencia
Aunque pareciera que una circunferencia no tiene una pendiente constante debido a su forma curva, en realidad cada punto de la circunferencia tiene una pendiente constante respecto a la tangente en ese punto. La pendiente en cada punto es perpendicular al radio en ese mismo punto.
3. Parábola
La parábola es una curva que puede tener una pendiente constante en algunos puntos. Por ejemplo, la parábola con la ecuación y = x^2 tiene una pendiente constante de 2 en todos los puntos donde la tangente es perpendicular al eje x.
4. Hipérbola
La hipérbola es una curva que también puede tener una pendiente constante en algunos puntos. Por ejemplo, la hipérbola con la ecuación y = 1/x tiene una pendiente constante de -1 en todos los puntos donde la tangente es perpendicular al eje x.
5. Elipse
La elipse es otra curva que puede tener una pendiente constante en algunos puntos. La pendiente en cada punto de la elipse varía dependiendo de la relación entre los semiejes mayor y menor.
Estos son solo algunos ejemplos de lugares geométricos con pendiente constante. La geometría ofrece una amplia variedad de figuras y curvas con diferentes características y propiedades.
Aplicaciones de los lugares geométricos con pendiente constante
Los lugares geométricos con pendiente constante son un concepto fundamental en la geometría analítica. Estos lugares son formas o curvas que representan todos los puntos que tienen una pendiente específica con respecto a una referencia dada, como una línea recta o un plano.
Una de las aplicaciones más comunes de los lugares geométricos con pendiente constante es en la construcción de carreteras. Cuando se traza una carretera recta, es esencial que tenga una pendiente constante para garantizar la seguridad y la estabilidad del camino. Usando los conceptos de lugares geométricos con pendiente constante, ingenieros y urbanistas pueden diseñar carreteras que cumplan con los estándares de pendiente necesarios.
Otra aplicación importante se encuentra en la planificación de sistemas de riego. Al diseñar sistemas de riego agrícola, es esencial garantizar que el agua fluya de manera eficiente y uniforme a través de los cultivos. Los lugares geométricos con pendiente constante pueden ayudar a determinar las pendientes necesarias en los canales de riego y asegurar que el agua se distribuya de manera adecuada.
Además, los lugares geométricos con pendiente constante también encuentran aplicaciones en la construcción de edificios. Los arquitectos y los ingenieros estructurales utilizan estos conceptos para diseñar escaleras y rampas con pendientes constantes que cumplan con los estándares de accesibilidad y seguridad.
En resumen, los lugares geométricos con pendiente constante tienen una amplia gama de aplicaciones en diversas áreas como la ingeniería civil, la agricultura y la arquitectura. Estos conceptos son esenciales para garantizar la correcta planificación y diseño de estructuras y sistemas.
Conclusión
En resumen, al utilizar las etiquetas HTML en las frases más importantes del texto, estamos resaltando su importancia y llamando la atención del lector hacia ellas. La etiqueta enfatiza el texto y lo hace más prominente visualmente.
Además, al combinar las etiquetas con el uso de encabezados H3, podemos organizar y jerarquizar la información de manera efectiva. Los encabezados H3 son útiles cuando queremos destacar subsecciones dentro de un artículo o blog post.
También, es posible emplear listas en HTML para presentar información de manera estructurada y legible. Las listas pueden ser ordenadas (
- ) o no ordenadas (
- ), y dentro de ellas podemos utilizar las etiquetas de negrita () para resaltar elementos importantes.
En conclusión, al utilizar correctamente las etiquetas HTML , los encabezados H3, las listas en HTML y las negritas (), podemos mejorar la legibilidad y la organización de nuestros textos, haciéndolos más atractivos y efectivos para el lector.