Características esenciales de la mediatriz de un segmento

¿Qué es la mediatriz de un segmento y cuál es su importancia?

La mediatriz de un segmento es la línea perpendicular que pasa por su punto medio. En otras palabras, es la línea que divide el segmento en dos partes iguales y forma ángulos rectos con él.

La importancia de la mediatriz radica en varias aplicaciones en geometría y en la resolución de problemas geométricos. Algunas de estas aplicaciones son:

• Determinar el punto medio: La mediatriz nos permite encontrar el punto medio de un segmento de manera precisa, dividiéndolo exactamente en dos partes iguales.
• Construcción de triángulos: La mediatriz es esencial para construir triángulos equiláteros, ya que sus tres mediatrices se intersectan en un punto llamado circuncentro.
• Encontrar puntos equidistantes: Si trazamos perpendiculares a la mediatriz desde cualquier punto del segmento, los puntos donde estas perpendiculares intersectan a la mediatriz estarán equidistantes del punto original.
• Resolver problemas de congruencia: La mediatriz puede utilizarse para demostrar que dos segmentos son congruentes, es decir, tienen la misma longitud.

En resumen, la mediatriz de un segmento es una línea muy útil en geometría que nos permite determinar el punto medio, construir triángulos equiláteros, encontrar puntos equidistantes y resolver problemas de congruencia. Su importancia radica en su aplicación práctica en diferentes situaciones geometrías.

Propiedades de la mediatriz de un segmento

La mediatriz de un segmento es la recta perpendicular que pasa por el punto medio del segmento. Esta recta tiene algunas propiedades importantes que vale la pena mencionar:

1. La mediatriz divide al segmento en dos partes iguales. Esto significa que la distancia desde cualquier punto de la mediatriz hasta los extremos del segmento es la misma.
2. La mediatriz es perpendicular al segmento. Esto implica que el ángulo que forma la mediatriz con el segmento es de 90 grados.
3. La mediatriz de un segmento es única. Esto quiere decir que solo hay una recta que cumple todas estas propiedades y que pasa por el punto medio del segmento.
4. Si una recta es perpendicular a una mediatriz y pasa por uno de los extremos del segmento, entonces también pasa por el otro extremo del segmento.

Estas propiedades son fundamentales cuando se trabaja con segmentos en geometría. La mediatriz nos permite encontrar el punto medio de un segmento y también nos brinda información sobre simetrías y ángulos de 90 grados.

Metodos para trazar la mediatriz de un segmento

En geometría, la mediatriz de un segmento es la recta perpendicular que divide al segmento en dos partes iguales. Trazar la mediatriz de un segmento puede ser útil en diversos contextos, como la construcción de triángulos o la resolución de problemas geométricos.

Método 1: Utilizando una regla y compás

Para trazar la mediatriz de un segmento utilizando una regla y compás, sigue los siguientes pasos:

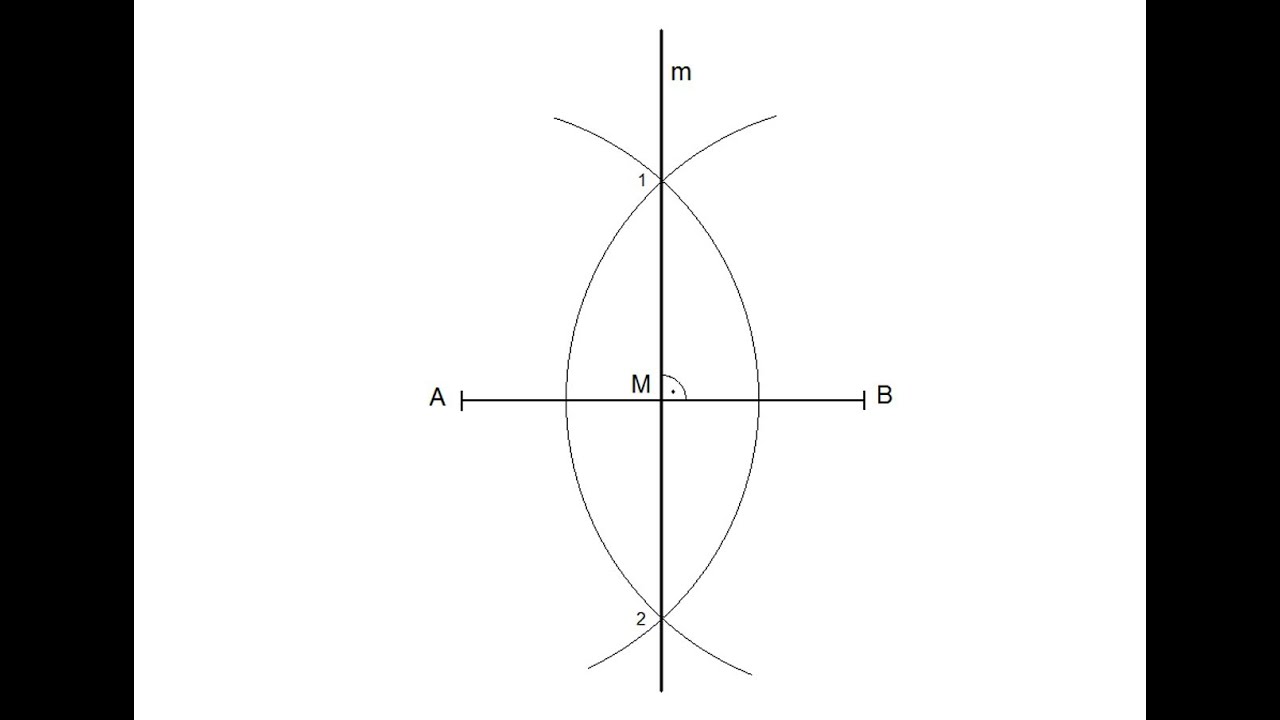
1. Dibuja el segmento que deseas trazar la mediatriz.
2. Con el compás, coloca la punta en uno de los extremos del segmento y dibuja un arco que atraviese el segmento.
3. Repite el paso 2 desde el otro extremo del segmento, asegurándote de que el arco intersecte al anterior.
4. Con la regla, une los puntos donde los arcos se cruzan. La línea recta resultante será la mediatriz del segmento.

Método 2: Utilizando un programa de geometría dinámica

Otra opción es utilizar un programa de geometría dinámica, como Geogebra, que permite construir y visualizar objetos geométricos de manera interactiva. Con este tipo de software, trazar la mediatriz de un segmento es aún más sencillo:

1. Abre el programa de geometría dinámica.
2. Dibuja el segmento que deseas trazar la mediatriz.
3. Selecciona la herramienta correspondiente a la mediatriz.
4. Haz clic en uno de los extremos del segmento y luego en el otro extremo.
5. El programa trazará automáticamente la mediatriz del segmento.

Método 3: Utilizando un compás y una recta auxiliar

Una alternativa es utilizar un compás y una recta auxiliar para trazar la mediatriz:

1. Dibuja el segmento que deseas trazar la mediatriz.
2. Utiliza la regla para dibujar una recta auxiliar que atraviese el segmento en un punto cualquiera.
3. Con el compás, dibuja un arco desde uno de los extremos del segmento que corte a la recta auxiliar.
4. Repite el paso 3 desde el otro extremo del segmento.
5. Con la regla, une los puntos de intersección de los arcos. La línea recta resultante será la mediatriz del segmento.

Estos son algunos métodos comunes para trazar la mediatriz de un segmento. La elección del método dependerá de las herramientas disponibles y la preferencia personal. ¡Explora y diviértete construyendo geometría!

Aplicaciones prácticas de la mediatriz de un segmento

La mediatriz de un segmento es la recta perpendicular que pasa por el punto medio de dicho segmento. Aunque puede parecer un concepto matemático abstracto, tiene aplicaciones prácticas en diferentes campos. A continuación, se presentan algunas de las aplicaciones más comunes:

1. Construcción de triángulos equiláteros

La mediatriz de un segmento puede utilizarse como una herramienta para construir triángulos equiláteros. Dado un segmento, se traza su mediatriz, luego se toma un punto cualquiera sobre ella y se trazan dos arcos de igual radio desde este punto en cada dirección. Donde se corten los arcos, se unen los puntos con el punto inicial del segmento, y así se obtiene un triángulo equilátero.

2. Ubicación de objetos en un mapa

En topografía o cartografía, la mediatriz de un segmento es útil para ubicar objetos en un mapa. Dado un área y dos puntos conocidos dentro de ella, se traza la mediatriz del segmento formado por esos dos puntos. El objeto buscado estará ubicado en algún punto de esta mediatriz.

3. Delimitación de terrenos

En propiedad de la tierra, la mediatriz de un segmento puede ser utilizada para delimitar terrenos. Si se conocen los puntos extremos de un lote de tierra, se traza la mediatriz de ese segmento. La mediatriz actúa como una línea divisoria equidistante de los puntos extremos, lo que permite una delimitación justa y equitativa del terreno entre diferentes propietarios.

4. Resolución de problemas de geometría

La mediatriz de un segmento también tiene aplicación en la resolución de problemas de geometría. Por ejemplo, puede ser utilizada para encontrar el centro de un círculo circunscrito a un triángulo. La mediatriz de cada lado del triángulo se interseca en un punto que es el centro del círculo circunscrito.

5. Equilibrio de fuerzas

En física, la mediatriz de un segmento puede utilizarse en el análisis del equilibrio de fuerzas. Si se tiene un cuerpo rígido sujeto a dos fuerzas de igual magnitud pero en direcciones opuestas, la mediatriz del segmento formado por las líneas de acción de estas fuerzas representa la línea de acción de una fuerza resultante nula, indicando que el cuerpo estará en equilibrio.

Conclusiones sobre las características esenciales de la mediatriz de un segmento

La mediatriz de un segmento es una línea perpendicular que pasa por el punto medio del segmento. A continuación, presentamos algunas conclusiones importantes sobre las características esenciales de la mediatriz:

1. Perpendicularidad: La mediatriz es siempre perpendicular al segmento que divide.
2. Pasa por el punto medio: La mediatriz pasa por el punto medio del segmento que divide, es decir, equidista de los extremos del segmento.
3. Simetría: La mediatriz divide al segmento en dos partes iguales, creando una simetría entre los puntos del segmento respecto a la mediatriz.
4. Intersección: La mediatriz de un segmento se intersecta con otras mediatrices de segmentos en un punto común llamado circuncentro del triángulo formado por los tres puntos extremos de los segmentos.
5. Identificación: La mediatriz puede ser identificada con una construcción geométrica utilizando un compás y una regla, trazando arcos de radio igual a la mitad de la longitud del segmento desde los extremos del segmento hacia el exterior.

En resumen, la mediatriz de un segmento es una línea perpendicular que pasa por el punto medio del segmento, divide el segmento en dos partes iguales, crea una simetría entre los puntos del segmento y se intersecta con otras mediatrices en el circuncentro. Es una construcción geométrica importante que se utiliza en diversos conceptos matemáticos y en la resolución de problemas geométricos.