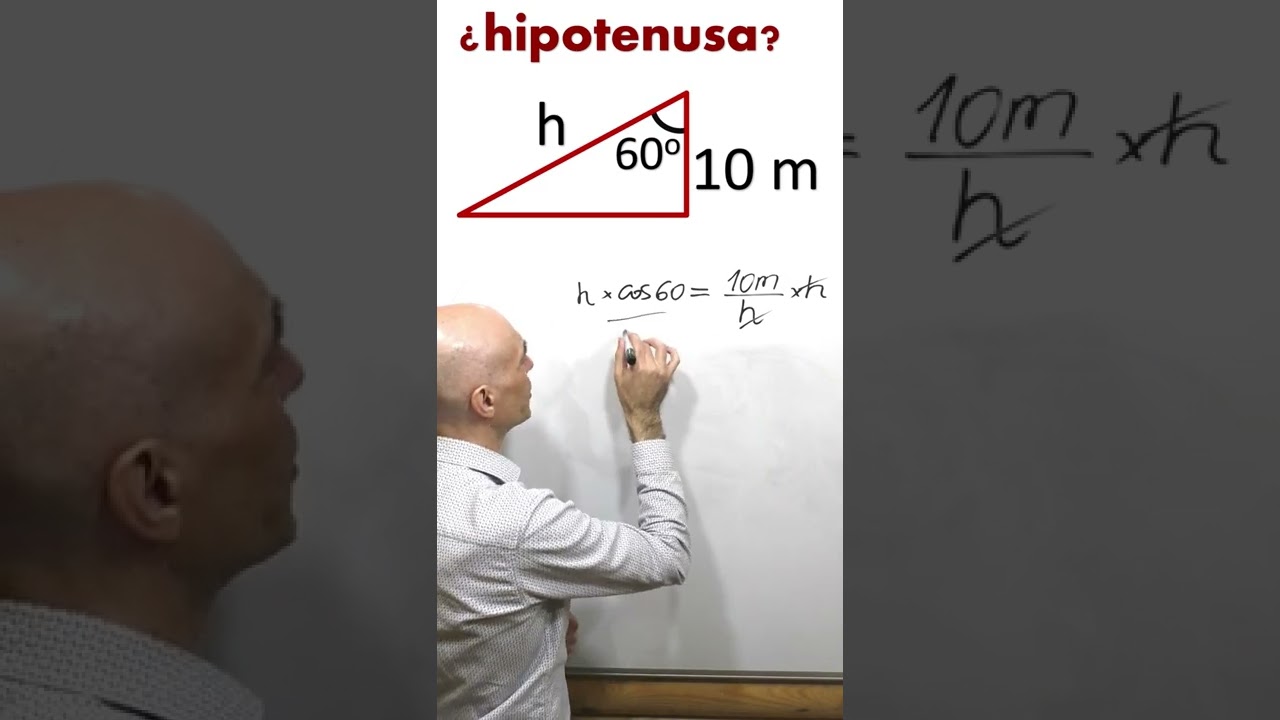
El concepto de cociente trigonométrico
Los cocientes obtenidos al dividir las longitudes de los lados de un triángulo rectángulo son fundamentales en trigonometría. En particular, el cociente entre el cateto adyacente y la hipotenusa es de gran importancia y tiene aplicaciones extensas en diversos campos de la ciencia y la ingeniería.
El cateto adyacente y la hipotenusa
Antes de explorar el cociente en cuestión, es crucial comprender los elementos de un triángulo rectángulo. El cateto adyacente es el lado que forma un ángulo con respecto a un ángulo agudo en el triángulo, mientras que la hipotenusa es el lado opuesto al ángulo recto, siendo el lado más largo del triángulo rectángulo.
Definición del cociente
El cociente obtenido al dividir el cateto adyacente entre la hipotenusa se conoce como el coseno del ángulo agudo en el triángulo rectángulo. Este cociente está estrechamente relacionado con las propiedades de los ángulos y las razones trigonométricas, y su comprensión es esencial en el estudio de la trigonometría y la geometría.
Representación trigonométrica
La representación trigonométrica de un ángulo agudo en un triángulo rectángulo se basa en el cociente mencionado. Esta representación proporciona una forma de relacionar las longitudes de los lados del triángulo con las funciones trigonométricas, lo que es fundamental para resolver problemas tanto teóricos como prácticos.
Relación con otras funciones trigonométricas
El cociente del cateto adyacente entre la hipotenusa no solo está vinculado al coseno de un ángulo, sino que también interactúa con otras funciones trigonométricas como el seno y la tangente. Esta interrelación es crucial para comprender las propiedades de los triángulos rectángulos y resolver problemas trigonométricos complejos.
Aplicaciones en ingeniería
En ingeniería, el conocimiento de los cocientes trigonométricos es fundamental para diversos campos, incluyendo la mecánica, la construcción y la electrónica. Por ejemplo, al calcular fuerzas o tensiones en estructuras, la relación entre los lados de un triángulo rectángulo puede desempeñar un papel crucial en la determinación de la estabilidad y la seguridad de las construcciones.
En la navegación marítima y la cartografía, el cociente entre el cateto adyacente y la hipotenusa es esencial para navegar con precisión. La determinación de la ubicación y el trazado de rutas se basa en gran medida en el uso de las funciones trigonométricas, lo que destaca la importancia de este cociente en situaciones del mundo real.
Relación con el teorema de Pitágoras
El famoso teorema de Pitágoras, que establece la relación entre los lados de un triángulo rectángulo, está estrechamente relacionado con el cociente del cateto adyacente entre la hipotenusa. La comprensión de esta relación proporciona una visión más profunda de los principios fundamentales de la geometría y la trigonometría.
Impacto en la tecnología moderna
En la era actual, el uso de dispositivos electrónicos y sistemas de comunicación implica el uso de conceptos trigonométricos, incluido el cociente mencionado. Desde el diseño de antenas hasta la programación de algoritmos, la comprensión de las relaciones trigonométricas es esencial en el desarrollo y la innovación tecnológica.
Desarrollos matemáticos y científicos
El estudio de los cocientes trigonométricos ha dado lugar a avances significativos en matemáticas puras y aplicadas. La extrapolación de estas relaciones a contextos más amplios ha permitido el desarrollo de teoremas y métodos matemáticos que tienen aplicaciones en campos tan diversos como la física, la economía y la biología.
Utilidad en la resolución de problemas
La comprensión de los cocientes trigonométricos, incluyendo el cociente del cateto adyacente entre la hipotenusa, es esencial para resolver una amplia gama de problemas en matemáticas y ciencias aplicadas. Desde la predicción de fenómenos naturales hasta la optimización de procesos industriales, estos conceptos son una herramienta invaluable para los investigadores y profesionales.
Importancia en la educación
La enseñanza y el aprendizaje de los cocientes trigonométricos desempeñan un papel crucial en la formación de estudiantes en disciplinas STEM (ciencia, tecnología, ingeniería y matemáticas). Promover una comprensión sólida de estos conceptos desde las etapas educativas tempranas sienta las bases para el desarrollo de habilidades analíticas y la resolución de problemas en el futuro.
Consideraciones finales
En resumen, el cociente obtenido al dividir el cateto adyacente entre la hipotenusa es un concepto fundamental en trigonometría con aplicaciones amplias y significativas en diversas áreas del conocimiento. Su comprensión es crucial para el desarrollo de la ciencia, la tecnología y la ingeniería, y su relevancia perdura en la resolución de problemas cotidianos y el avance del conocimiento humano.
Referencias
1. Stewart, J. (2015). Trigonometry. Cengage Learning.
2. Larson, R., & Battaglia, S. M. (2010). Trigonometry. Cengage Learning.