¿Qué es un dominio de una función con raíz?
En matemáticas, el dominio de una función con raíz es el conjunto de valores para los cuales la función está definida. En otras palabras, es el conjunto de números que puedes introducir en la función para obtener un resultado válido.
Un dominio de una función con raíz puede estar restringido debido a las restricciones de la función raíz. Por ejemplo, si tienes una función raíz cuadrada, el dominio estaría limitado a números reales no negativos, ya que no se pueden realizar operaciones de raíz cuadrada de números negativos en el conjunto de números reales.
Por otra parte, si tienes una función raíz cúbica, el dominio estaría compuesto por todos los números reales, ya que se pueden realizar operaciones de raíz cúbica para cualquier número real.
Para identificar el dominio de una función con raíz, es importante prestar atención a las restricciones de la función. Estas restricciones pueden ser indicadas a través de limitaciones en los exponentes o en los argumentos de la función raíz.
En resumen, el dominio de una función con raíz es el conjunto de valores para los cuales la función está definida y puede dar un resultado válido. Al analizar el dominio, es necesario tener en cuenta las restricciones de la función raíz.
Conceptos básicos sobre funciones con raíz
En matemáticas, una función con raíz es aquella en la que la variable x se encuentra dentro de una raíz, como por ejemplo la función raíz cuadrada (√x) o la función raíz cúbica (∛x).
Para comprender mejor estos conceptos, es importante recordar qué es una raíz. La raíz de un número es aquel valor que, al ser elevado a una potencia determinada, resulta en el número original. Por ejemplo, la raíz cuadrada de 9 es 3, ya que 3 elevado al cuadrado es igual a 9.
Las funciones con raíz permiten encontrar el valor de x para el cual se cumple una determinada ecuación. Por ejemplo, si tenemos la ecuación √x = 4, la función nos permitirá encontrar el valor de x que hace que la raíz cuadrada de x sea igual a 4.
Es importante tener en cuenta que cuando trabajamos con raíces en funciones, existen ciertas restricciones. Por ejemplo, la raíz cuadrada solo puede ser aplicada a números no negativos, ya que no existe una raíz cuadrada de un número negativo en el conjunto de los números reales.
En la resolución de funciones con raíz, es común utilizar métodos como la elevación al cuadrado o al cubo, así como el despeje de la variable x. Esto nos permitirá encontrar las soluciones posibles para la ecuación dada.
En conclusión, las funciones con raíz son una herramienta matemática útil para resolver ecuaciones en las que la variable x se encuentra dentro de una raíz. Es importante tener en cuenta las restricciones y utilizar métodos apropiados para encontrar las soluciones de la ecuación.
Cálculo del dominio de una función con raíz
En el cálculo del dominio de una función con raíz, es importante tener en cuenta que la raíz de cualquier número real no está definida si el exponente de la raíz es un número impar y el radicando es negativo. Por lo tanto, para encontrar el dominio de una función con raíz, debemos asegurarnos de evitar esos valores.
Una forma común de representar una función con raíz es a través de la ecuación y = √x. En este caso, el dominio de la función está determinado por los valores de x que hacen que la raíz esté definida.
Para evitar que el radicando sea negativo, podemos establecer una restricción en la ecuación y decir que x debe ser mayor o igual a cero (x ≥ 0). De esta forma, nos aseguramos de que la raíz sea siempre un número real.
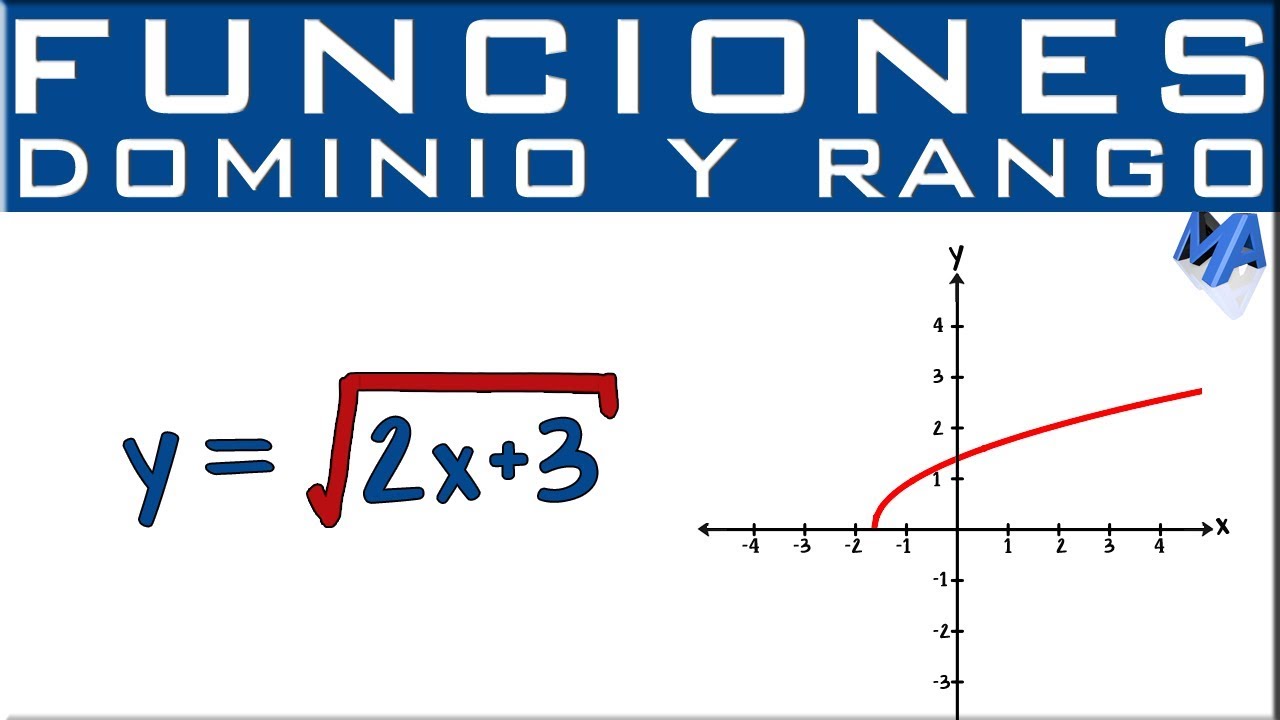
Además, también es importante tener en cuenta que algunas funciones con raíz pueden tener más restricciones adicionales. Por ejemplo, en la función y = √(x – 2), además de la restricción de x ≥ 0, también debemos tener en cuenta que x – 2 debe ser mayor o igual a cero (x - 2 ≥ 0). Esto nos lleva a otra restricción de x ≥ 2.
En resumen, para calcular el dominio de una función con raíz, debemos asegurarnos de evitar valores de x que hagan que el radicando sea negativo. Además, también debemos considerar cualquier restricción adicional que pueda estar presente en la función.
Ejemplo: Cálculo del dominio de una función con raíz
Tomemos como ejemplo la función y = √(x – 5). Para calcular el dominio de esta función, debemos establecer las restricciones necesarias.
La primera restricción es que x – 5 debe ser mayor o igual a cero (x - 5 ≥ 0). Esto nos lleva a la restricción x ≥ 5.
Por lo tanto, el dominio de la función y = √(x – 5) es x ≥ 5.
En conclusión, el cálculo del dominio de una función con raíz requiere tener en cuenta las restricciones para evitar valores de x que hagan que el radicando sea negativo. Estas restricciones pueden variar dependiendo de la función en particular. Es importante seguir estos pasos para garantizar la definición de la función en todo su dominio.
Ejemplos prácticos de cálculo del dominio
En esta sección, presentaremos cuatro ejemplos prácticos para calcular el dominio de una función. Estos ejemplos te ayudarán a comprender mejor este concepto fundamental en el estudio de las matemáticas.
Ejemplo 1:
Consideremos la función f(x) = √(x-2). Para determinar el dominio de esta función, recordamos que la raíz cuadrada solo es válida para valores mayores o iguales a cero. Por lo tanto, debemos encontrar los valores de x para los cuales x-2 ≥ 0. Despejando la ecuación, obtenemos x ≥ 2. Por lo tanto, el dominio de f(x) es [2, ∞).
Ejemplo 2:
Tomemos la función g(x) = 1/(x+3). En este caso, debemos evitar la división por cero. Por lo tanto, encontramos los valores de x para los cuales x+3 ≠ 0. Restando 3 en ambos lados de la ecuación, obtenemos x ≠ -3. Por lo tanto, el dominio de g(x) es (-∞, -3) ∪ (-3, ∞).
Ejemplo 3:
Ahora examinemos la función h(x) = log(x-1). En este caso, el logaritmo solo está definido para valores estrictamente mayores a cero. Por lo tanto, debemos encontrar los valores de x para los cuales x-1 > 0. Sumando 1 en ambos lados de la ecuación, obtenemos x > 1. Por lo tanto, el dominio de h(x) es (1, ∞).
Ejemplo 4:
Por último, consideremos la función j(x) = tan(x). La función tangente está definida para todos los valores de x excepto aquellos donde el coseno es igual a cero. Por lo tanto, encontramos los valores de x para los cuales cos(x) ≠ 0. Estos valores son x ≠ (2n+1)π/2, donde n es un número entero. Por lo tanto, el dominio de j(x) es {x | x ≠ (2n+1)π/2, n ∈ ℤ}.
En conclusión, a lo largo de este artículo hemos explorado diferentes aspectos relacionados con el uso de etiquetas HTML. Hemos aprendido sobre la importancia de utilizar etiquetas como <strong> para resaltar frases importantes en un texto.
El uso de la etiqueta <strong> sirve para dar énfasis a ciertas palabras o frases, haciéndolas más destacadas y resaltantes para el lector. Esto es especialmente útil cuando queremos enfatizar información vital o crucial en un artículo.
Adicionalmente, hemos mencionado el uso de <h3> para crear encabezados de tercer nivel. Estos encabezados nos permiten organizar el contenido de nuestro texto de manera jerárquica y facilitar la lectura y comprensión para nuestros lectores.
Asimismo, se ha hecho mención de las listas en HTML, las cuales pueden ser creadas mediante las etiquetas <ul> (para listas no ordenadas) y <ol> (para listas ordenadas). Estas etiquetas nos permiten presentar información de manera estructurada y fácil de seguir.
En resumen, el uso adecuado de etiquetas HTML como <strong>, <h3>, y el empleo de listas en HTML, son herramientas fundamentales para mejorar la presentación y la estructura de nuestros contenidos en la web.