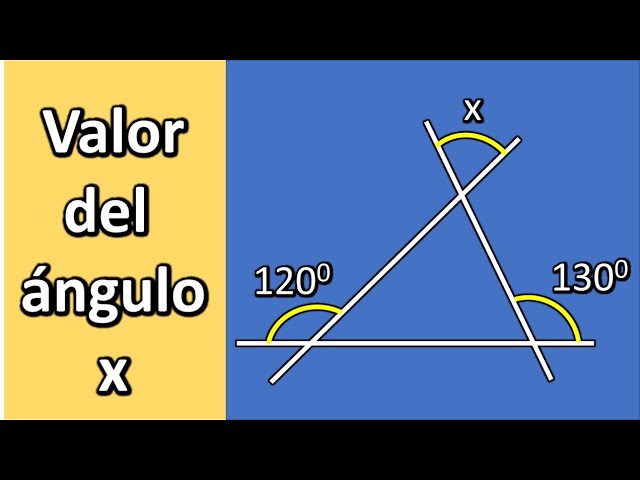
Analizando el diagrama
En el mundo de la geometría, los ángulos son una parte fundamental, y comprender su valor en grados es esencial para resolver problemas y desarrollar habilidades matemáticas. En este caso, nos enfrentamos a un diagrama que presenta un ángulo desconocido, representado por la letra «z». Para descubrir su medida, debemos seguir un proceso de análisis y aplicación de conceptos geométricos que nos permitirán desentrañar su valor con precisión.
Identificando elementos clave
Antes de abordar el valor de «z», es crucial identificar los elementos del diagrama que nos brindarán pistas sobre el ángulo en cuestión. Observamos líneas rectas, intersecciones y posiblemente ángulos conocidos que nos ayudarán a resolver el enigma de «z». Cada detalle importa y nos guiará en el camino hacia la solución.
Aplicando conceptos geométricos
La geometría es una disciplina rica en conceptos y teoremas que nos brindan herramientas para comprender la relación entre líneas, ángulos y figuras geométricas. Al aplicar estos principios, podremos desglosar el diagrama y utilizar nuestra comprensión para determinar el valor de «z».
Utilizando teoremas y propiedades
Dentro del vasto repertorio geométrico, existen teoremas y propiedades que nos permiten resolver incógnitas como la que nos plantea el ángulo «z». La aplicación de estos conceptos fortalecerá nuestra capacidad para abordar el problema de manera sistemática, guiándonos hacia la respuesta precisa que buscamos.
Midiendo ángulos conocidos
Para resolver el enigma de «z», es probable que necesitemos comenzar por medir ángulos conocidos dentro del diagrama. Estas medidas nos proporcionarán puntos de referencia fundamentales para encauzar nuestra resolución y avanzar hacia la determinación del ángulo desconocido.
Trabajando con líneas perpendiculares
Las líneas perpendiculares también pueden desempeñar un papel crucial en la resolución del valor de «z». Al comprender cómo interactúan estas líneas en el diagrama, podremos utilizar sus intersecciones para establecer relaciones angulares que nos acerquen a la solución.
Considerando la suma de ángulos en un triángulo
Otro enfoque importante es considerar la suma de ángulos en un triángulo. Dado que el diagrama podría contener triángulos u otras figuras, este concepto nos brinda la oportunidad de aplicar la regla angular fundamental y utilizarla como medio para calcular el ángulo «z».
Empleando la ley de los senos y cosenos
En ciertos contextos, la ley de los senos y cosenos puede ser una herramienta invaluable para determinar ángulos en un triángulo o en configuraciones más complejas. Al reconocer las posibles aplicaciones de estas leyes en el diagrama, ampliamos nuestro espectro de recursos para abordar el desafío de encontrar el valor de «z».
Desarrollando ecuaciones angulares
La representación de ángulos desconocidos a través de ecuaciones angulares es una estrategia efectiva para resolver problemas geométricos. Al plantear ecuaciones relacionadas con los ángulos presentes en el diagrama, podemos avanzar hacia la resolución de «z» de manera estructurada y organizada.
Aplicando el teorema del ángulo externo
El teorema del ángulo externo es otro recurso valioso que puede proporcionar información clave sobre ángulos específicos en una figura geométrica. Al considerar su aplicación en el contexto del diagrama, podemos desbloquear claves fundamentales para descifrar el enigma de «z».
Explorando la simetría y congruencia
La simetría y la congruencia son conceptos que juegan un papel vital en la geometría, y su relevancia se extiende al análisis de ángulos en un diagrama. Al buscar patrones simétricos y aplicar principios de congruencia, podemos revelar relaciones angulares que nos conduzcan a la solución que buscamos.
Integrando el uso de ángulos suplementarios y complementarios
Los ángulos suplementarios y complementarios pueden proporcionar información esencial para resolver problemas geométricos. Al reconocer oportunidades para aplicar estas relaciones angulares dentro del diagrama, fortalecemos nuestra capacidad para abordar el desafío de determinar el valor de «z».
Investigando relaciones proporcionales
La presencia de segmentos o proporciones en el diagrama podría revelar relaciones angulares proporcionales que nos acerquen a la medida de «z». Al explorar estas posibles relaciones, ampliamos nuestra perspectiva y enriquecemos nuestras herramientas para resolver el enigma planteado.
Culminando en la solución
Después de aplicar cuidadosamente los diversos conceptos y estrategias geométricas, llegamos al momento esperado: la determinación del valor en grados del ángulo «z». Al reunir todas las piezas del rompecabezas y utilizar nuestra comprensión geométrica de manera efectiva, finalmente desvelamos el misterio y revelamos el valor preciso de este ángulo.
La resolución del valor en grados del ángulo «z» en el diagrama nos ha llevado a un fascinante viaje a través de conceptos geométricos, teoremas y estrategias de resolución de problemas. Esta exploración nos ha permitido no solo calcular un ángulo desconocido, sino también fortalecer nuestra comprensión de la geometría y su aplicabilidad en situaciones desafiantes. Este ejercicio demuestra el poder y la relevancia de la geometría en la resolución de incógnitas, invitándonos a abrazar su belleza y utilidad en nuestro viaje matemático.