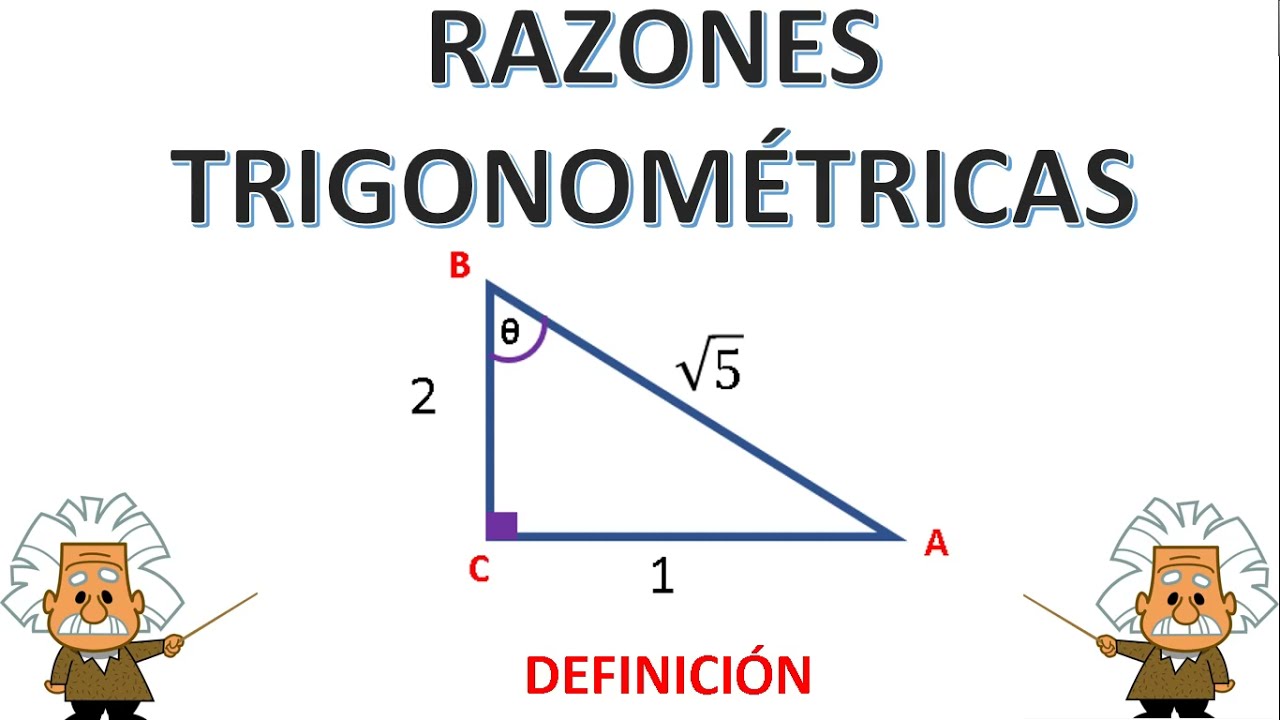
La razón trigonométrica es un concepto fundamental en matemáticas y geometría, especialmente en el estudio de las relaciones entre los ángulos de un triángulo y sus lados. Las razones trigonométricas, que incluyen el seno, el coseno y la tangente, son herramientas esenciales para resolver problemas de trigonometría y para comprender fenómenos naturales y científicos.
Importancia de las razones trigonométricas
Las razones trigonométricas son fundamentales en diversas áreas como la ingeniería, la física, la astronomía, la arquitectura y la navegación, entre otras. Estas razones proporcionan un marco teórico para entender y modelar fenómenos relacionados con el movimiento, la ondulación, la oscilación y la propagación de ondas, que son comunes en la naturaleza y en aplicaciones humanas. Además, las razones trigonométricas son esenciales para resolver problemas de medición, posicionamiento y diseño de estructuras.
Las tres razones trigonométricas principales
Las tres razones trigonométricas principales son el seno, el coseno y la tangente, cada una de las cuales está relacionada con un ángulo en un triángulo rectángulo:
Seno
El seno de un ángulo agudo en un triángulo rectángulo se define como la longitud del cateto opuesto dividida por la longitud de la hipotenusa. Matemáticamente, el seno de un ángulo θ se representa como sin(θ) = longitud del cateto opuesto / longitud de la hipotenusa.
Coseno
El coseno de un ángulo agudo en un triángulo rectángulo se define como la longitud del cateto adyacente dividida por la longitud de la hipotenusa. Matemáticamente, el coseno de un ángulo θ se representa como cos(θ) = longitud del cateto adyacente / longitud de la hipotenusa.
Tangente
La tangente de un ángulo agudo en un triángulo rectángulo se define como la longitud del cateto opuesto dividida por la longitud del cateto adyacente. Matemáticamente, la tangente de un ángulo θ se representa como tan(θ) = longitud del cateto opuesto / longitud del cateto adyacente.
Relaciones entre las razones trigonométricas
Las razones trigonométricas están interrelacionadas mediante diversas identidades trigonométricas, que permiten expresar una razón en función de otras. Estas relaciones son útiles para simplificar o transformar expresiones trigonométricas, lo que facilita la resolución de ecuaciones y problemas geométricos y físicos. Algunas de las identidades más comunes incluyen la identidad pitagórica, la relación entre seno y coseno (identidad fundamental) y las identidades de ángulo doble y medio.
Identidad Pitagórica
La identidad pitagórica establece la relación fundamental entre los lados de un triángulo rectángulo. Según esta identidad, en un triángulo rectángulo con ángulos agudos θ, el seno y el coseno satisfacen la ecuación fundamental: sen²(θ) + cos²(θ) = 1. Esta relación es derivada directamente del teorema de Pitágoras y es fundamental para comprender la geometría y la trigonometría.
Relación entre seno y coseno
La relación entre seno y coseno, conocida como identidad fundamental, establece una conexión significativa entre estas dos razones trigonométricas. Matemáticamente, para cualquier ángulo θ, se cumple que sen(θ) = √(1 – cos²(θ)) y cos(θ) = √(1 – sen²(θ)). Esta relación es esencial para simplificar expresiones trigonométricas y para transformar entre las diferentes razones trigonométricas.
Aplicaciones de las razones trigonométricas
Las razones trigonométricas tienen numerosas aplicaciones en el mundo real, especialmente en disciplinas que involucran mediciones y modelado de fenómenos naturales y artificiales. Algunas de las aplicaciones prácticas incluyen la navegación marítima, el diseño arquitectónico, el análisis de estructuras, la astronomía, la ingeniería de sonido, la manipulación de señales y el estudio del movimiento oscilatorio y ondulatorio.
En la navegación marítima, las razones trigonométricas son fundamentales para determinar la ubicación y el rumbo de una embarcación en el mar. Mediante el uso de herramientas como sextantes y cartas náuticas, los navegantes pueden aplicar las razones trigonométricas para calcular la distancia y la dirección entre diferentes puntos geográficos, lo que es crucial para la navegación segura y precisa.
Diseño arquitectónico y análisis de estructuras
En el diseño arquitectónico y el análisis de estructuras, las razones trigonométricas son utilizadas para calcular medidas angulares, determinar la estabilidad y resistencia de edificaciones, y modelar el comportamiento de elementos estructurales sometidos a cargas y fuerzas. El uso de las razones trigonométricas permite a los arquitectos, ingenieros civiles y constructores desarrollar estructuras seguras y eficientes.
Estudio del movimiento oscilatorio y ondulatorio
En la física y la ingeniería, las razones trigonométricas son esenciales para analizar y modelar el movimiento oscilatorio y ondulatorio, como el movimiento armónico simple, las ondas sonoras, las ondas electromagnéticas y las ondas mecánicas. Las funciones trigonométricas, incluidas las razones trigonométricas, son utilizadas para describir y predecir el comportamiento de estas formas de movimiento y propagación de ondas.
Resolución de problemas trigonométricos
Las razones trigonométricas son fundamentales para resolver problemas geométricos y trigonométricos que involucran ángulos y medidas de distancias. A través de la aplicación de las razones trigonométricas y las identidades relacionadas, es posible determinar longitudes de lados, calcular áreas de regiones, encontrar alturas de objetos y resolver ecuaciones que involucran funciones trigonométricas. Estas habilidades son valiosas en diferentes disciplinas académicas y profesionales, incluyendo la geometría, la trigonometría, la física y la ingeniería.
Ejemplo de resolución de un problema trigonométrico
Supongamos que queremos calcular la altura de un edificio utilizando la razón trigonométrica del coseno. Si conocemos la distancia horizontal desde un punto de observación hasta la base del edificio, y el ángulo de elevación desde el punto de observación hasta la parte superior del edificio, podemos aplicar la razón trigonométrica del coseno para encontrar la altura del edificio.
Si el ángulo de elevación es θ y la distancia horizontal es d, entonces la altura h del edificio se puede encontrar utilizando la expresión h = d * cos(θ). Al utilizar el coseno del ángulo de elevación, podemos calcular la altura del edificio sin necesidad de medir directamente la altura.
En resumen, las razones trigonométricas son conceptos matemáticos fundamentales que tienen aplicaciones extendidas en la ciencia, la ingeniería, la arquitectura y otras disciplinas. Comprender las razones trigonométricas y saber cómo aplicarlas es crucial para resolver problemas geométricos, modelar fenómenos naturales y realizar mediciones precisas. Al dominar estos conceptos, los estudiantes y profesionales pueden desarrollar habilidades sólidas en el análisis matemático y la resolución de problemas prácticos. Las razones trigonométricas proporcionan un marco teórico poderoso para comprender diversas áreas del conocimiento y para abordar desafíos del mundo real.