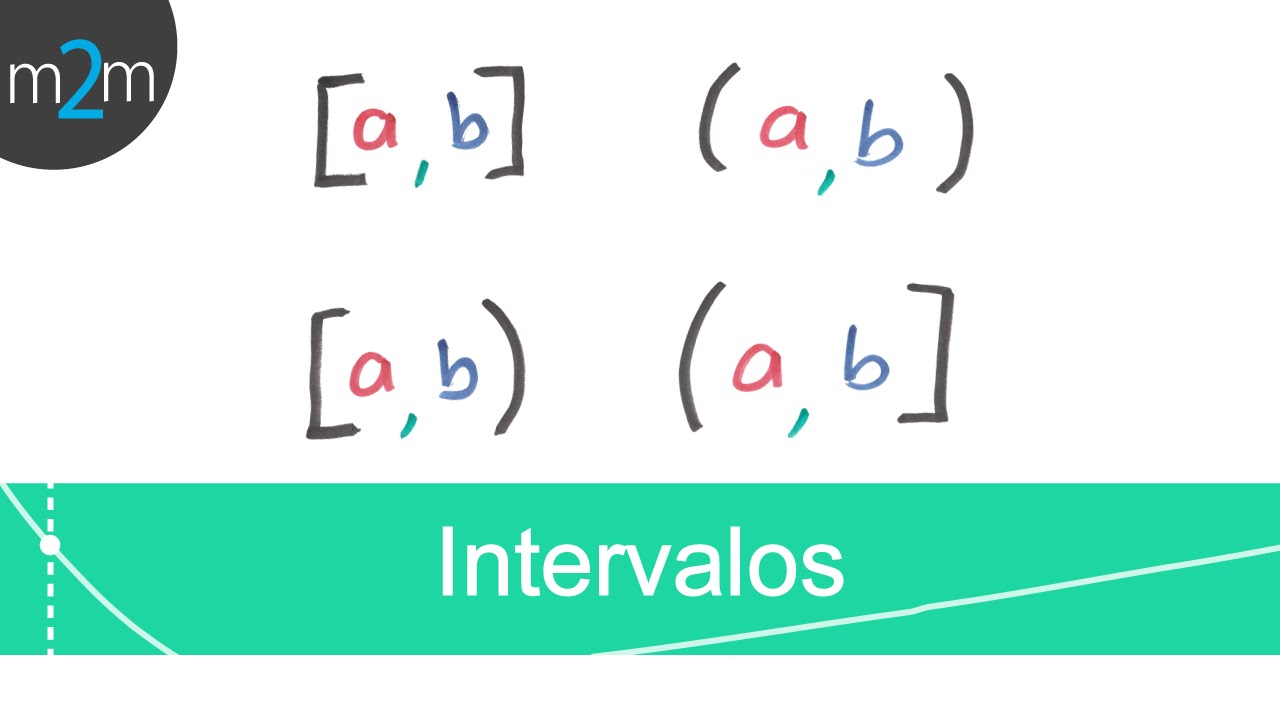
1. ¿Qué es un intervalo abierto?
Un intervalo abierto es un conjunto de números reales que incluye todos los valores entre dos números extremos, pero no incluye los propios extremos. Se representa generalmente como un par ordenado (a, b), donde a y b son los números extremos del intervalo.
Por ejemplo, el intervalo abierto (2, 5) incluye todos los números reales mayores que 2 y menores que 5, pero no incluye los propios números 2 y 5.
Los intervalos abiertos son muy utilizados en matemáticas y tienen varias aplicaciones en diferentes áreas. Por ejemplo, en cálculo diferencial se utilizan para definir el límite de una función en un punto.
Características de un intervalo abierto:
- No incluye los extremos: Como mencioné anteriormente, los intervalos abiertos no incluyen los números extremos. Esto se debe a que el conjunto solo abarca los valores entre los dos extremos.
- Puede ser infinito: Un intervalo abierto puede ser infinito en alguna o en ambas direcciones. Por ejemplo, (0, ∞) representa todos los números reales mayores que cero.
- Puede ser acotado: Un intervalo abierto también puede ser acotado, es decir, tener un límite inferior y un límite superior. Por ejemplo, (-5, 5) incluye todos los números reales entre -5 y 5.
Es importante tener en cuenta que los intervalos abiertos se diferencian de los intervalos cerrados y semiabiertos, ya que en estos últimos se incluyen uno o ambos extremos.
2. ¿Qué es un intervalo cerrado?
En matemáticas, un intervalo cerrado es un conjunto de números que incluye su punto de inicio y su punto final. Se representa mediante paréntesis cuadrados, también conocidos como corchetes. Por ejemplo, [2, 5] es un intervalo cerrado que va desde el número 2 hasta el número 5.
La principal característica de un intervalo cerrado es que incluye todos los valores dentro de él, es decir, tanto el punto de inicio como el punto final son considerados parte del intervalo. Esto se diferencia de un intervalo abierto, el cual no incluye los extremos.
Los intervalos cerrados son utilizados en diversas ramas de las matemáticas, como el cálculo y el análisis matemático. Son especialmente útiles para describir rangos de valores o conjuntos numéricos específicos.
Es importante tener en cuenta que los intervalos cerrados pueden ser infinitos, es decir, no tienen un límite superior o inferior. Por ejemplo, el intervalo [-∞, ∞] representa todos los números reales
.
3. Características del intervalo abierto
Un intervalo abierto es un conjunto de números reales que se caracteriza por tener dos extremos con infinitas posibilidades entre ellos, sin incluir dichos extremos en el conjunto. En otras palabras, se representa como (a, b), donde a y b son los extremos del intervalo.
Las principales características de un intervalo abierto son:
- No incluye los extremos: A diferencia de los intervalos cerrados, un intervalo abierto no incluye los extremos. Esto significa que los valores a y b no pertenecen al conjunto.
- Infinitos valores intermedios: Entre los extremos a y b del intervalo abierto existen infinitas posibilidades de valores intermedios. Esto se debe a que no hay límites en cuanto a la cantidad de números reales que pueden existir entre los dos extremos.
- Ejemplos de notación: La notación más común para representar un intervalo abierto es mediante paréntesis, como (a, b). También se puede utilizar la notación de intervalo con rayas, como a < x < b.
Es importante tener en cuenta estas características al utilizar intervalos abiertos en conceptos matemáticos y también al trabajar con ellos en problemas o ecuaciones.
4. Características del intervalo cerrado
En matemáticas, un intervalo cerrado es aquel que incluye tanto su punto inicial como su punto final. Tiene varias características importantes:
1. El intervalo cerrado se representa mediante paréntesis cuadrados, como [a, b]. Esto indica que los valores de a y b están incluidos en el intervalo.
2. El punto inicial del intervalo, a, es el valor más pequeño dentro del intervalo, mientras que el punto final, b, es el valor más grande.
3. Todos los valores comprendidos entre a y b también están incluidos en el intervalo cerrado.
4. El intervalo cerrado es un conjunto de infinitos números que están ordenados de menor a mayor. No hay ningún número real entre el punto inicial y el punto final que no esté incluido en el intervalo.
5. El intervalo cerrado es una forma de describir un conjunto de números reales de manera completa y precisa. Al indicar los puntos inicial y final, se delimita claramente qué valores se encuentran dentro del intervalo.
En resumen, el intervalo cerrado es una forma de representar un conjunto de números reales de manera completa y precisa, incluyendo tanto su punto inicial como su punto final, así como todos los valores que están entre ellos.
5. Diferencias entre intervalo abierto y cerrado
En matemáticas, los intervalos son conjuntos de números que están comprendidos entre dos valores. Y dentro de los intervalos, podemos encontrar dos tipos principales: los intervalos abiertos y los intervalos cerrados. A continuación, veremos cuáles son las diferencias entre ellos:
Intervalo Abierto
Un intervalo abierto es aquel en el cual los extremos no están incluidos en el intervalo. Esto quiere decir que el primer número del intervalo no se considera parte del mismo, así como tampoco el último número.
Podemos representar un intervalo abierto mediante el uso de paréntesis. Por ejemplo, el intervalo abierto (3, 7) incluiría todos los números mayores a 3 y menores a 7.
Algunas características de los intervalos abiertos son:
- No incluye los extremos del intervalo.
- Se representan con paréntesis.
- Se lee como “mayor que” y “menor que”.
Intervalo Cerrado
Por otro lado, un intervalo cerrado es aquel en el cual los extremos están incluidos en el intervalo. Esto significa que tanto el primer número como el último número del intervalo son parte del mismo.
Los intervalos cerrados se representan utilizando corchetes. Por ejemplo, el intervalo cerrado [0, 5] incluiría todos los números mayores o iguales a 0 y menores o iguales a 5.
Algunas características de los intervalos cerrados son:
- Incluye los extremos del intervalo.
- Se representan con corchetes.
- Se lee como “mayor o igual que” y “menor o igual que”.
En resumen, la diferencia principal entre los intervalos abiertos y cerrados radica en si se incluyen o no los extremos del intervalo. Los intervalos abiertos no los incluyen, mientras que los intervalos cerrados sí los incluyen. Ambos tipos de intervalos tienen sus usos y aplicaciones específicas en diferentes ramas de las matemáticas y la ciencia.