«`html
La distribución de muestreo de la media es un concepto fundamental en estadísticas que nos permite comprender la variabilidad de las medias muestrales al extraer repetidamente muestras de una población. En este artículo, exploraremos en detalle este concepto crucial y su aplicación en la inferencia estadística.
La importancia de la distribución de muestreo de la media
La distribución de muestreo de la media juega un papel esencial en la inferencia estadística. Cuando queremos hacer afirmaciones sobre una población utilizando muestras, es crucial entender cómo se distribuyen las medias de esas muestras. Esto nos permite hacer inferencias precisas sobre parámetros poblacionales basándonos en la información de las muestras.
Imagina que queremos saber la media de altura de todos los estudiantes de una universidad, pero medir a cada estudiante es impracticable. En cambio, tomamos muestras de estudiantes y calculamos la media de cada muestra. La distribución de muestreo de la media nos ayudará a comprender qué tan cercanas están esas medias muestrales a la verdadera media de la población y con qué variabilidad.
La población y la muestra
Antes de sumergirnos en la distribución de muestreo de la media, es crucial comprender dos conceptos fundamentales: la población y la muestra. La población se refiere al conjunto completo de observaciones que estamos estudiando, mientras que la muestra es un subconjunto representativo de la población que utilizamos para hacer inferencias.
Dentro del contexto de la distribución de muestreo de la media, la población es el conjunto completo de todos los posibles valores de la variable en estudio, mientras que la muestra es un subconjunto de esos valores seleccionados para el análisis. Es importante que la muestra sea representativa de la población para que las conclusiones que extrapolemos de ella sean válidas.
Tamaño de la muestra y precisión
El tamaño de la muestra juega un papel crítico en la distribución de muestreo de la media. En general, a medida que el tamaño de la muestra aumenta, la distribución de las medias muestrales se aproxima más a una distribución normal, lo que facilita la inferencia estadística. Un tamaño de muestra grande tiende a proporcionar estimaciones más precisas de la media poblacional.
Por otro lado, si la muestra es demasiado pequeña, la distribución de las medias muestrales puede no ser simétrica o tender a una distribución normal. Esto puede dificultar la inferencia sobre la población. Por lo tanto, elegir el tamaño de muestra adecuado es crucial para obtener conclusiones confiables a partir de la distribución de muestreo de la media.
La distribución normal y el teorema del límite central
La distribución de muestreo de la media está estrechamente relacionada con la distribución normal y el teorema del límite central. El teorema del límite central establece que, independientemente de la forma de la distribución de la población, la distribución de las medias muestrales tiende a seguir una distribución normal a medida que el tamaño de la muestra aumenta.
Este resultado es fundamental, ya que nos permite hacer suposiciones sobre la distribución de las medias muestrales incluso si la distribución de la población no es normal. La distribución normal es altamente predecible y comprensible, lo que facilita la inferencia estadística basada en las medias muestrales.
El cálculo de la distribución de muestreo de la media
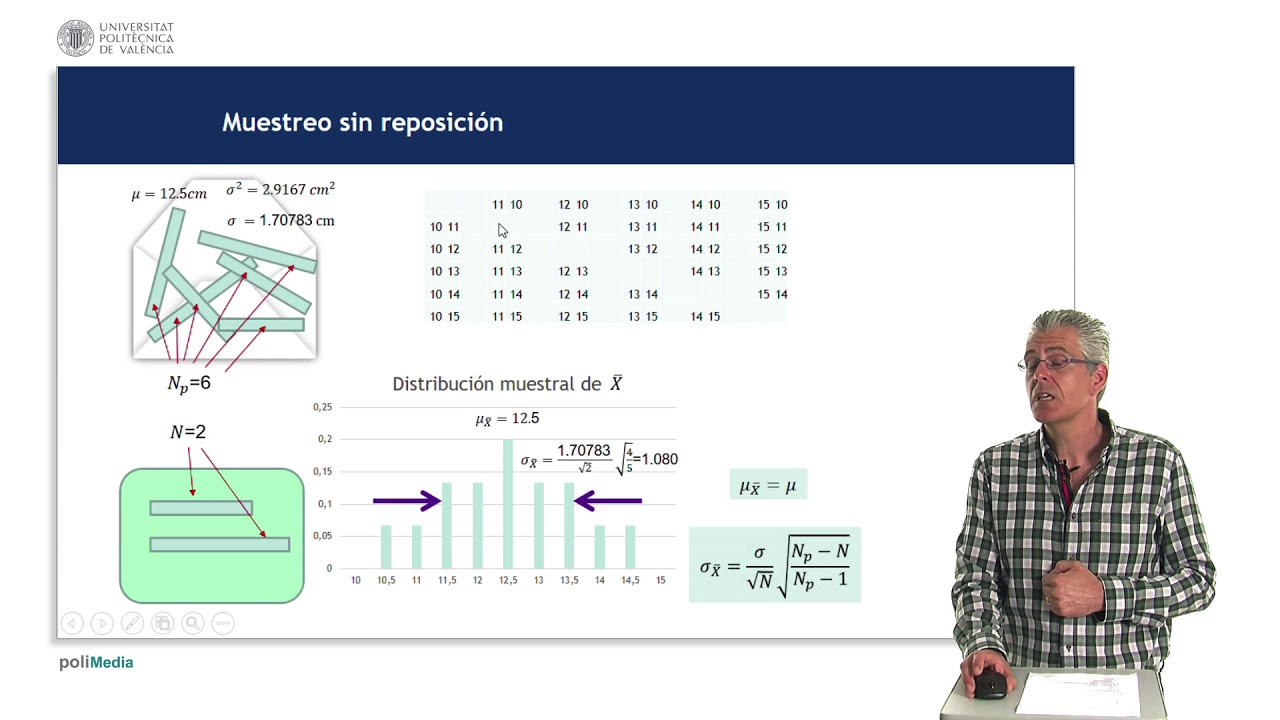
Calcular la distribución de muestreo de la media implica determinar la media y la desviación estándar de todas las posibles muestras de un tamaño dado tomadas de una población. Esta distribución resultante nos da información sobre la variabilidad de las medias muestrales que podríamos obtener al extraer repetidamente muestras de la población.
La media de la distribución de muestreo de la media es igual a la media poblacional, lo que refleja la no tendenciosidad del estimador de la media muestral. La desviación estándar de la distribución de muestreo de la media, conocida como error estándar, es inversamente proporcional a la raíz cuadrada del tamaño de la muestra, lo que significa que la variabilidad de las medias muestrales disminuye a medida que aumenta el tamaño de la muestra.
Intervalos de confianza y la distribución de muestreo de la media
Los intervalos de confianza son herramientas poderosas que nos permiten hacer inferencias sobre la media poblacional basándonos en la distribución de muestreo de la media. Un intervalo de confianza es un rango de valores alrededor de la media muestral que, con cierto nivel de confianza, contendrá la verdadera media poblacional.
La distribución de muestreo de la media nos proporciona la base para calcular estos intervalos de confianza. Al comprender la variabilidad de las medias muestrales, podemos determinar qué tan precisos son nuestros estimados de la media poblacional y con qué nivel de certeza podemos afirmar que el intervalo de confianza captura la verdadera media.
Pruebas de hipótesis y la distribución de muestreo de la media
Otro uso fundamental de la distribución de muestreo de la media es en las pruebas de hipótesis. Las pruebas de hipótesis nos permiten evaluar afirmaciones sobre parámetros poblacionales y tomar decisiones basadas en la evidencia de nuestras muestras. La distribución de muestreo de la media desempeña un papel crucial en la formulación de estas pruebas.
Al establecer una hipótesis nula y una alternativa, podemos utilizar la distribución de muestreo de la media para calcular el valor p, que nos indica la probabilidad de observar los datos muestrales si la hipótesis nula fuera cierta. Esto nos permite tomar decisiones informadas sobre aceptar o rechazar la hipótesis nula en función de la evidencia de nuestras muestras.
Aplicaciones prácticas de la distribución de muestreo de la media
La distribución de muestreo de la media tiene numerosas aplicaciones en la vida cotidiana y en una variedad de campos. En la investigación médica, por ejemplo, puede utilizarse para estipular intervalos de confianza para la eficacia de un tratamiento basándose en muestras de ensayos clínicos. En economía, puede aplicarse para estimar la media de ingresos de una población a partir de muestras de encuestas.
Incluso en el ámbito empresarial, comprender la distribución de muestreo de la media es esencial para tomar decisiones fundamentadas sobre el rendimiento de un producto o el comportamiento de los clientes. En resumen, esta herramienta estadística es invaluable en una amplia gama de escenarios, brindando una comprensión detallada de la variabilidad de las medias muestrales y su aplicabilidad en la inferencia estadística.
Conclusión
En definitiva, la distribución de muestreo de la media es un concepto fundamental en estadísticas que nos permite comprender la variabilidad de las medias muestrales y su aplicabilidad en la inferencia estadística. Al entender cómo se distribuyen las medias de las muestras extraídas de una población, podemos realizar afirmaciones precisas sobre parámetros poblacionales y tomar decisiones fundamentadas basadas en la evidencia de nuestras muestras.
«`