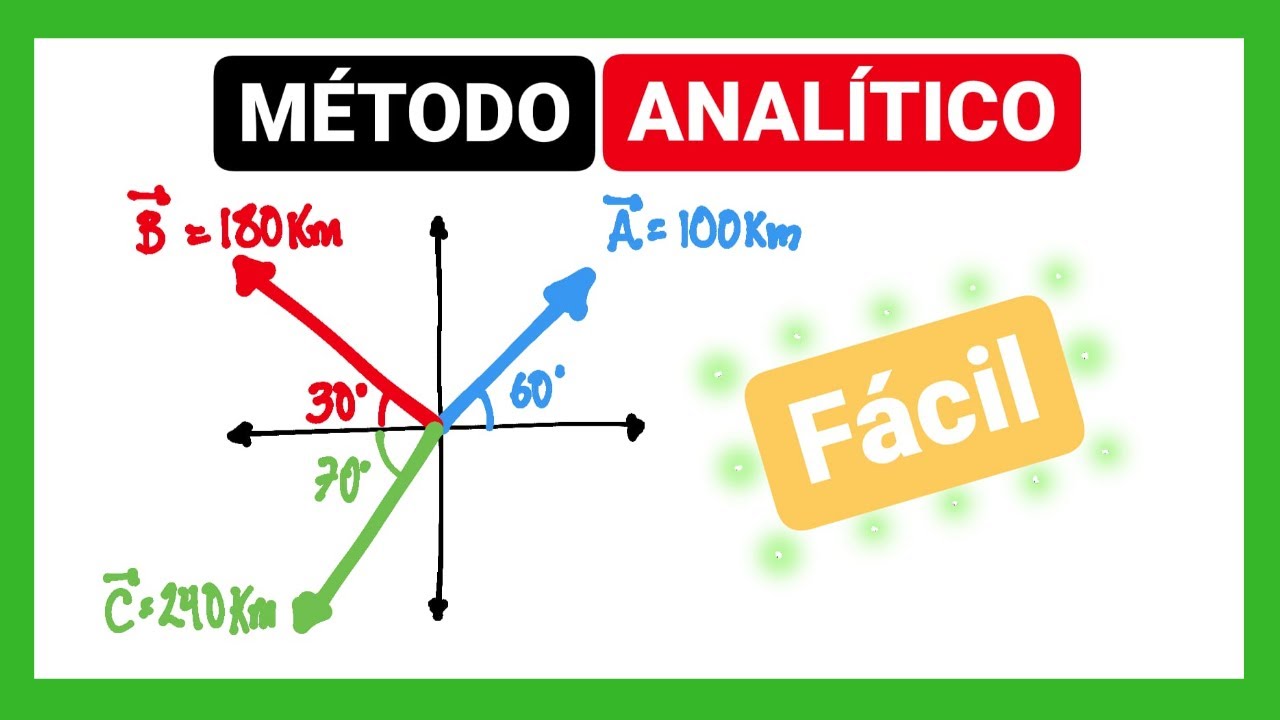
Ejemplo 1: Suma de dos vectores en el plano cartesiano
En el plano cartesiano, la suma de dos vectores se obtiene sumando sus componentes correspondientes.
Supongamos que tenemos dos vectores, A y B, definidos en el plano cartesiano:
- Vector A: (a1, a2)
- Vector B: (b1, b2)
Para obtener el vector suma, simplemente sumamos las componentes correspondientes:
Vector Suma: (a1 + b1, a2 + b2)
Por ejemplo, si tenemos los vectores A = (2, 3) y B = (4, -1), la suma sería:
- Suma de las componentes en la dirección x: 2 + 4 = 6
- Suma de las componentes en la dirección y: 3 + (-1) = 2
Por lo tanto, la suma de los vectores A y B sería:
Vector Suma = (6, 2)
De esta forma, podemos realizar la suma de dos vectores en el plano cartesiano siguiendo este procedimiento. Este ejemplo nos muestra cómo obtener la suma de dos vectores específicos, pero podemos aplicar el mismo procedimiento a cualquier par de vectores en el plano cartesiano.
Ejemplo 2: Suma de tres vectores en el espacio tridimensional
En este ejemplo vamos a calcular la suma de tres vectores en el espacio tridimensional.
Supongamos que tenemos tres vectores dados por:
- Vector A: A = [2, 1, -3]
- Vector B: B = [-1, 3, 2]
- Vector C: C = [4, -2, 1]
Para sumar estos vectores, simplemente debemos sumar componente por componente. Es decir, sumamos las componentes x, las componentes y y las componentes z.
La suma de los vectores A, B y C se calcula de la siguiente manera:
SUMA = [Ax + Bx + Cx, Ay + By + Cy, Az + Bz + Cz]
Aplicando la fórmula, obtenemos:
SUMA = [2 + (-1) + 4, 1 + 3 + (-2), -3 + 2 + 1]
Simplificando la suma, tenemos:
SUMA = [5, 2, 0]
Por lo tanto, la suma de los vectores A, B y C es SUMA = [5, 2, 0].
Ejemplo 3: Suma de vectores con diferente magnitud y dirección
En este ejemplo, vamos a hablar sobre la suma de vectores con diferente magnitud y dirección. Esto significa que vamos a tomar dos vectores, cada uno con un tamaño y una dirección diferente, y vamos a sumarlos.
¿Qué es un vector?
Un vector es una cantidad física que tiene magnitud y dirección. Puede representar cualquier cosa, como fuerzas, velocidades o desplazamientos. Los vectores se representan mediante flechas, donde la longitud de la flecha representa la magnitud del vector y la dirección de la flecha representa la dirección del vector.
¿Cómo se suman vectores?
Para sumar dos vectores con diferente magnitud y dirección, primero debemos descomponer los vectores en sus componentes x e y. Esto significa separar el vector en sus partes horizontales y verticales. Luego, sumamos las componentes x de ambos vectores y las componentes y de ambos vectores por separado. Esto nos dará las componentes x e y del vector resultante.
Una vez que tenemos las componentes x e y del vector resultante, podemos combinarlas para obtener el vector resultante. Esto se hace utilizando el teorema de Pitágoras, donde la magnitud del vector resultante es la raíz cuadrada de la suma de los cuadrados de las componentes x e y.
En resumen, para sumar vectores con diferente magnitud y dirección, seguimos estos pasos:
1. Descomponer los vectores en sus componentes x e y.
2. Sumar las componentes x de ambos vectores y las componentes y de ambos vectores por separado.
3. Utilizar el teorema de Pitágoras para combinar las componentes x e y y obtener la magnitud del vector resultante.
Ejemplo:
Supongamos que tenemos dos vectores: uno con una magnitud de 5 unidades y una dirección de 30 grados respecto al eje horizontal, y otro con una magnitud de 3 unidades y una dirección de 60 grados respecto al eje horizontal.
Para sumar estos dos vectores, primero descomponemos cada uno en sus componentes x e y. Luego, sumamos las componentes x y las componentes y por separado. Finalmente, combinamos las componentes x e y utilizando el teorema de Pitágoras para obtener la magnitud del vector resultante.
Después de realizar los cálculos, encontramos que el vector resultante tiene una magnitud de aproximadamente 7.81 unidades y una dirección de 47 grados respecto al eje horizontal.
En conclusión, la suma de vectores con diferente magnitud y dirección se puede realizar descomponiendo los vectores en sus componentes x e y, sumando las componentes por separado y luego combinando las componentes utilizando el teorema de Pitágoras. Esto nos dará la magnitud y la dirección del vector resultante.
Ejemplo 4: Suma de vectores utilizando componentes rectangulares
En este ejemplo, vamos a aprender cómo sumar vectores utilizando componentes rectangulares.
Paso 1: Conocer las componentes rectangulares de los vectores
Para sumar dos vectores utilizando componentes rectangulares, necesitamos conocer las componentes rectangulares de cada vector. Las componentes rectangulares son las magnitudes en las direcciones horizontal (x) y vertical (y).
Por ejemplo, si tenemos un vector A con componentes rectangulares Ax y Ay, y otro vector B con componentes rectangulares Bx y By, podemos sumarlos de la siguiente manera:
Paso 2: Sumar las componentes rectangulares
Para sumar las componentes rectangulares, simplemente sumamos las componentes correspondientes. Es decir, sumamos Ax con Bx y Ay con By:
- Ax + Bx para la componente horizontal (x)
- Ay + By para la componente vertical (y)
Esto nos dará las componentes rectangulares del vector suma C.
Paso 3: Obtener el vector suma
Una vez que tenemos las componentes rectangulares del vector suma C, podemos obtener el vector suma en sí. Simplemente escribimos las componentes rectangulares como C = (Cx, Cy).
Por ejemplo, si las componentes rectangulares del vector suma C son Cx = Ax + Bx y Cy = Ay + By, entonces el vector suma C es C = (Ax + Bx, Ay + By).
Así es como se realiza la suma de vectores utilizando componentes rectangulares. Recuerda siempre sumar las componentes correspondientes, tanto en la dirección horizontal (x) como en la dirección vertical (y).
Ejemplo 5: Suma de vectores utilizando el teorema de Pitágoras
En física, es común encontrarnos con situaciones en las que debemos sumar vectores para obtener un resultado final. Una forma de hacerlo es utilizando el teorema de Pitágoras, que nos permite calcular la magnitud de la suma de dos vectores.
Supongamos que tenemos dos vectores A y B, que se representan de la siguiente manera:
Para sumar estos dos vectores, primero debemos descomponerlos en sus componentes en el plano cartesiano. Si consideramos que el vector A tiene una magnitud de A y un ángulo θA con respecto al eje x, y el vector B tiene una magnitud de B y un ángulo θB con respecto al eje x, podemos escribirlos de la siguiente manera:
- A = Ax i + Ay j
- B = Bx i + By j
Para sumar los vectores A y B, simplemente debemos sumar sus componentes correspondientes:
- Ax = A * cos(θA)
- Ay = A * sin(θA)
- Bx = B * cos(θB)
- By = B * sin(θB)
Luego, sumamos las componentes en cada dirección para obtener las componentes del vector resultado:
- Rx = Ax + Bx
- Ry = Ay + By
Finalmente, utilizamos el teorema de Pitágoras para calcular la magnitud del vector resultado R:
|R| = sqrt((Rx)2 + (Ry)2)
De esta manera, podemos sumar vectores utilizando el teorema de Pitágoras.