Ejemplos prácticos de operaciones con punto decimal

Suma de números decimales

En el campo de las matemáticas, la suma es una operación fundamental que permite obtener la suma total o la adición de distintos números. En esta ocasión, nos enfocaremos en la suma de números decimales, los cuales son aquellos que contienen una parte fraccionaria.

¿Cómo se realiza la suma de números decimales?

La suma de números decimales se realiza de manera similar a la suma de números enteros. Se alinean los números decimales por su punto decimal y se procede a sumar las cifras de derecha a izquierda, llevando el “acarreo” cuando es necesario.

Por ejemplo, si deseamos sumar los números decimales 3.8 y 7.2, se alinean por el punto decimal y se suma cada cifra de manera correspondiente. El resultado sería 11.0.

Ejemplo de suma de números decimales

Veamos otro ejemplo práctico. Si queremos sumar los números decimales 2.45 y 1.8, se procedería de la siguiente manera:

• Se alinean los números por el punto decimal:
• 2.45
• + 1.8
• Se suman las cifras correspondientes de derecha a izquierda:
• 5
• + 8
• —–
• 3 (sin acarreo)
• + 4 (con acarreo)
• + 1
• El resultado de la suma sería 4.25.

En conclusión, la suma de números decimales es una operación matemática clave que permite obtener la suma total de números que contienen una parte fraccionaria. Con la correcta alineación de los números y la suma de las cifras, se puede obtener el resultado de manera precisa.

Resta de números decimales

La resta de números decimales es una operación aritmética básica que nos permite encontrar la diferencia entre dos números.

Para realizar la resta de números decimales, se siguen los mismos pasos que en la resta de números enteros. La diferencia principal radica en que debemos tener en cuenta la posición decimal de cada número.

Para restar números decimales, se alinean los dígitos de ambos números de tal manera que las posiciones decimales coincidan. Luego, se procede a restar cada dígito de derecha a izquierda, llevando hacia atrás cualquier “exceso” o “faltante” de la posición decimal.

Ejemplo:

Restar: 9.35 – 4.78

1. Alineamos los números:

9.35

– 4.78

2. Restamos empezando por los dígitos de la derecha:

9.35

– 4.78

0.57

El resultado de la resta de 9.35 y 4.78 es 0.57.

Es importante recordar que la resta de números decimales también puede generar números negativos si el minuendo es menor que el sustraendo.

En resumen, la resta de números decimales sigue los mismos principios que la resta de números enteros, pero teniendo en cuenta los lugares decimales de los números involucrados.

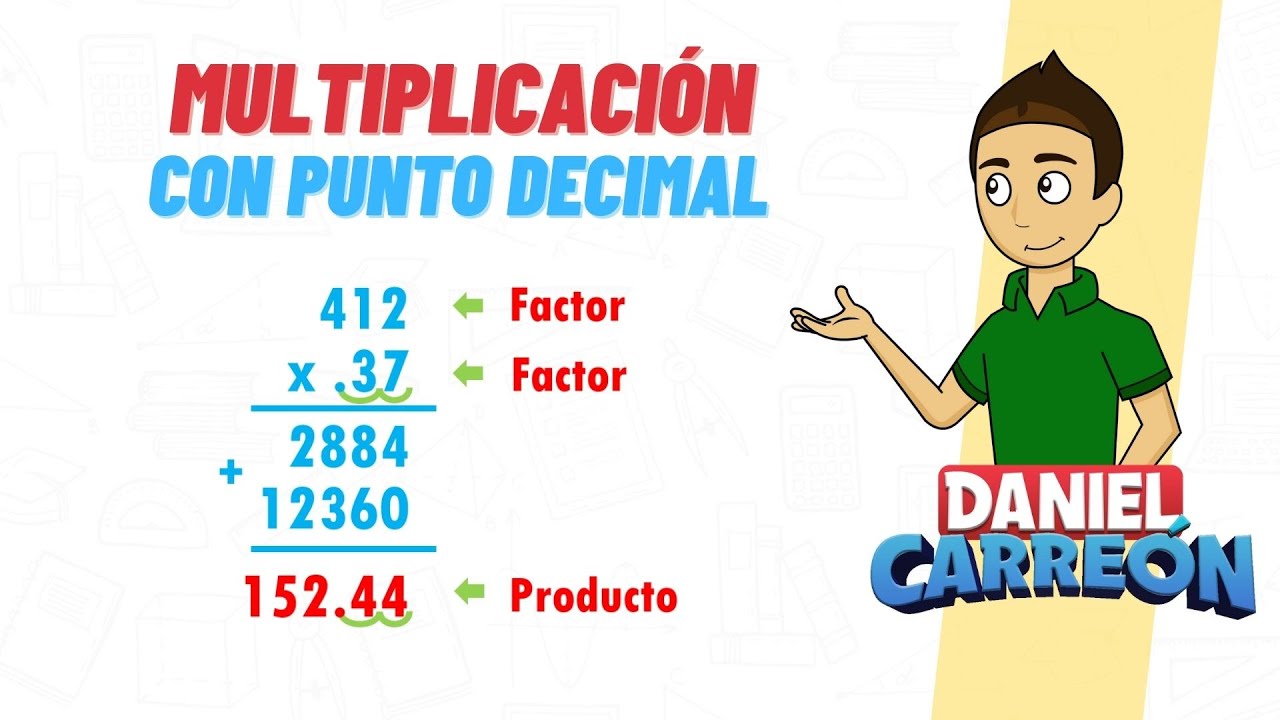
Multiplicación de números decimales

La multiplicación de números decimales es una operación matemática que se realiza para obtener el producto de dos o más números con parte decimal. Para llevar a cabo esta operación, se deben seguir ciertos pasos.

1. Paso 1: Coloca los números decimales uno debajo del otro, alineando las comas.
2. Paso 2: Realiza la multiplicación como si fueran números enteros, sin tener en cuenta las comas decimales.
3. Paso 3: Cuenta la cantidad de cifras decimales en total en los números que estás multiplicando.
4. Paso 4: Luego de obtener el producto de la multiplicación, coloca la coma decimal en el resultado contando desde la derecha tantas posiciones decimales como la suma de las cifras decimales de los números originales.

Por ejemplo, si queremos multiplicar 2.5 por 1.3, los pasos a seguir serían los siguientes:

Paso 1:
2.5
x 1.3

Paso 2:
     25
x   13
——
     325

Paso 3:
Los números originales tienen un total de 2 cifras decimales en total.

Paso 4:
Colocamos la coma decimal en el resultado a dos posiciones desde la derecha:
Resultado: 3.25

Recuerda que al multiplicar números decimales, es importante respetar la coma decimal y no olvidar contar las cifras decimales para colocar correctamente la coma en el resultado final.

División de números decimales

Cuando se trata de realizar divisiones con números decimales, es importante estar familiarizado con algunos conceptos básicos. Aquí te presentaremos algunos pasos clave para llevar a cabo esta operación de manera exitosa.

1. Coloca los números en el formato adecuado

Antes de comenzar a dividir, debes asegurarte de que los números estén en el formato correcto. Si alguno de los números no tiene la misma cantidad de decimales, deberás agregar ceros a la derecha hasta que ambos tengan la misma cantidad. Esto es crucial para obtener un resultado preciso.

2. Divide como si fueran números enteros

Una vez que los números tengan la misma cantidad de decimales, procede a realizar la división como si fueran números enteros. Coloca el divisor fuera del símbolo de división y el dividendo dentro. Realiza la operación como lo harías normalmente, llevando el cociente y el residuo.

3. Ajusta la coma decimal en el cociente

Después de obtener el cociente y el residuo, debes recordar colocar la coma decimal en el resultado final. Para hacer esto, mueve la coma decimal del dividendo hacia el cociente. Asegúrate de que la cantidad de decimales en el residuo sea igual a la cantidad de decimales que se encuentran en el cociente.

4. Simplifica si es necesario

En algunas ocasiones, es posible que el resultado de la división sea un número decimal periódico o una fracción. En esos casos, puedes decidir simplificar el resultado o dejarlo en su forma original, dependiendo de las necesidades del problema o la situación.

Recuerda practicar con diversos ejercicios para afianzar tu comprensión de este tema. Dividir números decimales puede parecer complicado al principio, pero con la práctica constante, podrás dominar esta habilidad matemática.

Aplicación de las operaciones con punto decimal en problemas cotidianos

Las operaciones con punto decimal son fundamentales en nuestra vida cotidiana, aunque a veces no nos damos cuenta de ello. Estas operaciones nos permiten realizar cálculos precisos y exactos cuando trabajamos con números decimales.

Suma y resta

Una de las aplicaciones más comunes de las operaciones con punto decimal es en las compras. Cuando vamos al supermercado y queremos calcular cuánto debemos pagar por varios productos que tienen precios con decimales, debemos utilizar la suma y la resta. Por ejemplo, si compramos dos productos que cuestan 3.99 y 2.50, debemos sumar estos dos números para obtener el total a pagar.

Multiplicación

Otra aplicación de las operaciones con punto decimal es en la cocina. Cuando seguimos una receta y necesitamos ajustar las cantidades de los ingredientes, debemos utilizar la multiplicación. Por ejemplo, si queremos preparar la mitad de una receta que requiere 1.5 tazas de harina, debemos multiplicar este número por 0.5 para obtener la cantidad correcta.

División

La división con punto decimal también es útil en situaciones cotidianas. Por ejemplo, cuando necesitamos calcular el costo por unidad de un producto para comparar precios. Si tenemos una caja de galletas que contiene 24 unidades y su precio es de 12.99, podemos dividir el costo total entre la cantidad de unidades para obtener el costo por unidad.

Razones y proporciones

Las razones y proporciones son otra forma de aplicar las operaciones con punto decimal en problemas cotidianos. Por ejemplo, si queremos saber cuántas millas recorremos por galón de gasolina en nuestro automóvil, podemos calcular la razón entre las millas recorridas y los galones de gasolina consumidos.

En resumen, las operaciones con punto decimal son fundamentales en nuestro día a día. Nos permiten realizar cálculos precisos y exactos en situaciones cotidianas como compras, cocina, comparar precios y calcular rendimientos. Es importante tener conocimientos sólidos en estas operaciones para poder desenvolvernos mejor en nuestro entorno.