El origen de las funciones trigonométricas
Las funciones trigonométricas son fundamentales en matemáticas y tienen una amplia gama de aplicaciones en diferentes campos, desde la física hasta la ingeniería. Su origen se remonta a la necesidad de estudiar y comprender las relaciones entre los ángulos y las longitudes de los lados de un triángulo, lo cual es esencial en la resolución de problemas prácticos.
La importancia de comprender las funciones trigonométricas
Conceptos básicos de trigonometría:
Antes de adentrarnos en el estudio de las funciones trigonométricas en ángulos de cualquier magnitud, es crucial tener una comprensión clara de los conceptos básicos de la trigonometría. Esto incluye entender las definiciones de seno, coseno, tangente, cotangente, secante y cosecante, así como sus relaciones con los lados de un triángulo rectángulo.
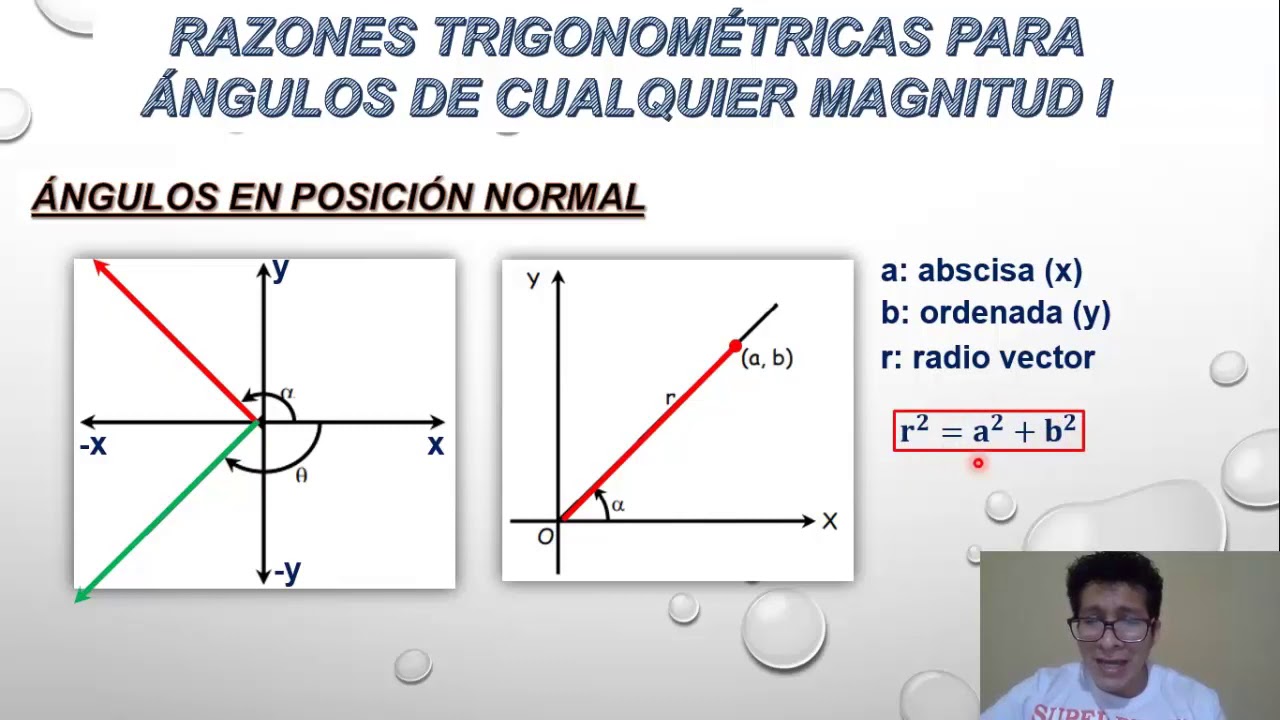
Extensión de las funciones trigonométricas a ángulos de cualquier magnitud
Definición de las funciones trigonométricas para ángulos agudos:
Las funciones trigonométricas son comúnmente definidas para ángulos agudos en un triángulo rectángulo. Sin embargo, es crucial comprender cómo estas funciones pueden extenderse para abarcar ángulos de cualquier magnitud, lo que nos permite explorar patrones y comportamientos más allá de los límites de un triángulo rectángulo convencional.
Relación entre las funciones trigonométricas y el círculo unitario
El círculo unitario como herramienta clave:
El círculo unitario juega un papel crucial al extender las funciones trigonométricas a ángulos de cualquier magnitud. Al trazar un círculo con radio igual a 1 en un sistema de coordenadas cartesianas, podemos visualizar las relaciones entre las funciones trigonométricas y los ángulos en un contexto más amplio. Esto nos brinda una poderosa herramienta para comprender las propiedades de estas funciones más allá de los triángulos rectángulos.
Comportamiento de las funciones trigonométricas en el círculo unitario
Gráficos y patrones:
Al trazar gráficos de las funciones trigonométricas en el círculo unitario, podemos observar patrones interesantes en la variación de estas funciones para ángulos de cualquier magnitud. Por ejemplo, la periodicidad y simetrías de seno y coseno, así como el comportamiento asintótico de las funciones tangente y cotangente, ofrecen una visión fascinante de cómo estas funciones se comportan en diferentes contextos.
Aplicaciones de las funciones trigonométricas en problemas del mundo real
Ingeniería y física:
Las funciones trigonométricas son esenciales en la resolución de problemas prácticos en campos como la ingeniería y la física. Desde el análisis de ondas y vibraciones hasta el diseño de estructuras y maquinaria, estas funciones nos permiten modelar y comprender fenómenos naturales y artificiales de manera precisa y eficiente.
El uso de tecnología para visualizar las funciones trigonométricas
Software de representación gráfica:
En la actualidad, contamos con una amplia gama de herramientas de software que nos permiten visualizar y explorar las funciones trigonométricas con gran detalle. Desde programas de cálculo matemático hasta aplicaciones interactivas en línea, estas herramientas brindan una perspectiva dinámica que facilita la comprensión de los conceptos y patrones relacionados con las funciones trigonométricas en ángulos de cualquier magnitud.
El papel de las transformaciones en el estudio de las funciones trigonométricas
Transformaciones básicas:
La capacidad de aplicar transformaciones a las funciones trigonométricas nos permite explorar cómo diferentes parámetros afectan la amplitud, el período y el desplazamiento de estas funciones. Comprender el impacto de estas transformaciones es fundamental para analizar y manipular eficazmente las funciones trigonométricas en diferentes contextos.
Aplicaciones de las transformaciones trigonométricas
Ingeniería de señales:
Las transformaciones trigonométricas desempeñan un papel crucial en el análisis y procesamiento de señales en ingeniería. Al aplicar transformaciones de frecuencia y amplitud a funciones trigonométricas, podemos extraer información útil y realizar operaciones como filtrado y modulación, lo que resulta fundamental en campos como las comunicaciones y la electrónica.
La conexión entre las transformaciones y el análisis armónico
Descomposición en series de Fourier:
Las transformaciones trigonométricas están estrechamente relacionadas con el análisis armónico, particularmente a través de la descomposición en series de Fourier. Esta poderosa técnica nos permite representar funciones periódicas como combinaciones de senos y cosenos, lo cual encuentra aplicaciones en la resolución de ecuaciones diferenciales y la generación de señales en sistemas de control y procesamiento de señales.
La importancia de la resolución de problemas en el estudio de las funciones trigonométricas
Aprendizaje basado en la resolución de problemas:
Al enfrentarse a desafíos matemáticos que implican el uso de funciones trigonométricas en situaciones variadas, los estudiantes pueden consolidar su comprensión conceptual y desarrollar habilidades analíticas y de razonamiento crítico. Resolver problemas prácticos relacionados con estas funciones es fundamental para internalizar y aplicar de manera efectiva los conceptos teóricos.
En conclusión, la extensión de las funciones trigonométricas a ángulos de cualquier magnitud nos brinda un marco poderoso para comprender y analizar patrones, comportamientos y aplicaciones en una variedad de campos. Desde su conexión con el círculo unitario hasta su papel en el análisis armónico y el procesamiento de señales, estas funciones siguen siendo fundamentales en la investigación y la práctica matemáticas, dejando un amplio espacio para la exploración y el descubrimiento de nuevas aplicaciones y conexiones con otros campos de estudio.