1. Introducción a las funciones trigonométricas
Las funciones trigonométricas son elementos fundamentales en el estudio de la geometría y el álgebra. Estas funciones se utilizan para describir las relaciones entre los ángulos y los lados de un triángulo.
En trigonometría, se trabajan principalmente con seis funciones: seno, coseno, tangente, cosecante, secante y cotangente. Estas funciones se representan matemáticamente con las letras sin, cos, tan, csc, sec y cot, respectivamente.
El seno de un ángulo se define como la razón entre la longitud del cateto opuesto y la hipotenusa. El coseno es la razón entre el cateto adyacente y la hipotenusa. Por otro lado, la tangente se obtiene dividiendo el cateto opuesto entre el cateto adyacente. Las funciones cosecante, secante y cotangente son los inversos de seno, coseno y tangente, respectivamente.
Estas funciones son periódicas, lo que significa que se repiten a lo largo del círculo trigonométrico. El círculo trigonométrico es una representación geométrica de las funciones trigonométricas. En él, el punto inicial se sitúa sobre el eje x positivo, y se va girando en sentido antihorario. Cada giro completo corresponde a 360 grados o 2π radianes.
En resumen, las funciones trigonométricas son herramientas poderosas para el análisis de triángulos y círculos. Su comprensión es fundamental en áreas como la física, la ingeniería, las matemáticas y la computación. Conocer y utilizar estas funciones nos permite resolver problemas que involucran ángulos y dimensiones espaciales de manera precisa y eficiente.
2. El círculo unitario: una herramienta fundamental en trigonometría
La trigonometría es una rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de un triángulo. Una herramienta fundamental en esta área es el círculo unitario, el cual juega un papel crucial en la resolución de problemas trigonométricos.
El círculo unitario es un círculo de radio 1 unidad, centrado en el origen de un sistema de coordenadas cartesianas. Se utiliza para visualizar las funciones seno y coseno de un ángulo en términos de sus coordenadas (x, y) en el círculo.
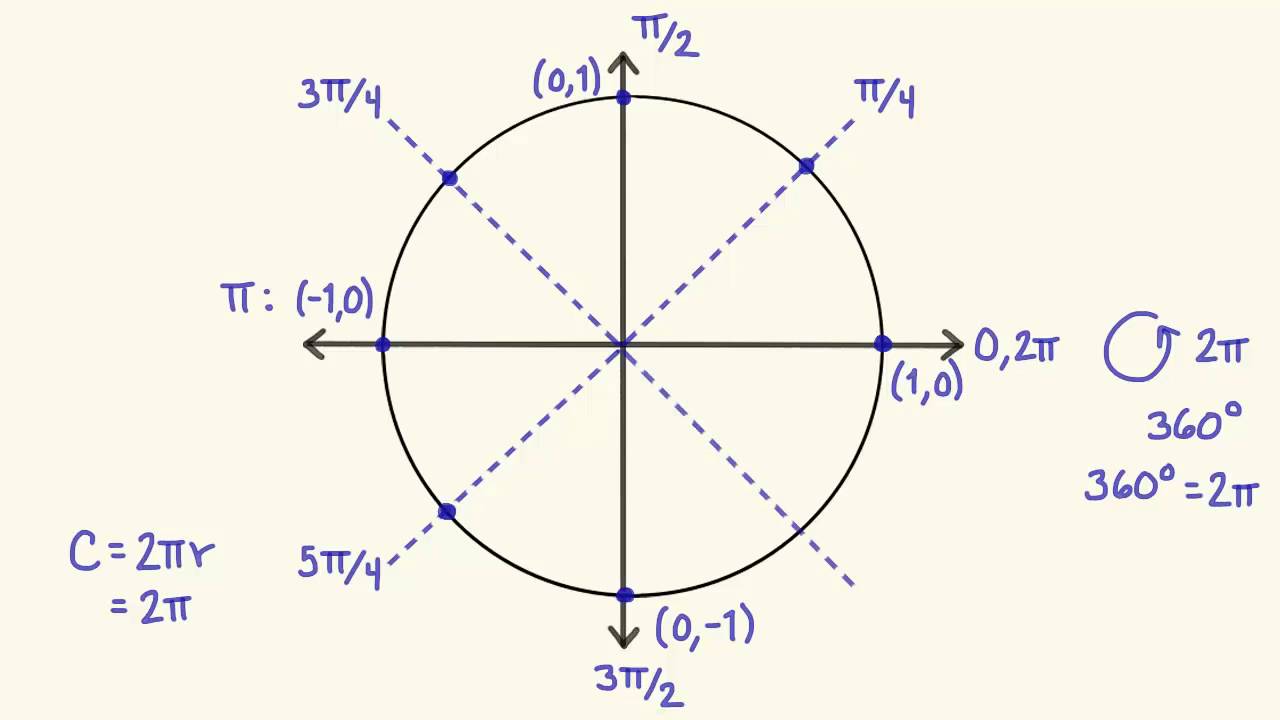
Al trazar un ángulo desde el origen hasta un punto en el círculo unitario, las coordenadas (x, y) de ese punto representan las razones trigonométricas del ángulo. El punto en el círculo, que corresponde al ángulo de 0 grados, tiene coordenadas (1, 0), lo que significa que el coseno de 0 grados es igual a 1 y el seno de 0 grados es igual a 0.
A medida que el ángulo aumenta en sentido antihorario, las coordenadas del punto cambian y, por lo tanto, también cambian las razones trigonométricas. Por ejemplo, cuando el ángulo es de 90 grados, el punto en el círculo tiene coordenadas (0, 1), lo que indica que el coseno de 90 grados es igual a 0 y el seno de 90 grados es igual a 1.
El círculo unitario también permite visualizar las identidades trigonométricas, que son ecuaciones que relacionan las funciones trigonométricas entre sí. Por ejemplo, la identidad fundamental de la trigonometría es:
Esta identidad se puede representar utilizando el círculo unitario: el coseno de un ángulo al cuadrado más el seno de ese mismo ángulo al cuadrado siempre es igual a 1.
En resumen, el círculo unitario es una herramienta esencial en trigonometría que permite visualizar y comprender las razones trigonométricas y las identidades trigonométricas. Su uso facilita la resolución de problemas trigonométricos y ayuda a los estudiantes a desarrollar una intuición visual sobre estas funciones matemáticas.
3. Funciones trigonométricas en el círculo unitario
Las funciones trigonométricas en el círculo unitario son herramientas fundamentales en matemáticas y física.
El círculo unitario se define como un círculo de radio 1 ubicado en el origen de un sistema de coordenadas cartesianas.
Seno
El seno de un ángulo en el círculo unitario se define como la coordenada y del punto en el círculo donde el ángulo intersecta el círculo.
Coseno
El coseno de un ángulo en el círculo unitario se define como la coordenada x del punto en el círculo donde el ángulo intersecta el círculo.
Tangente
La tangente de un ángulo en el círculo unitario se define como el cociente entre el seno y el coseno de ese ángulo.
Cotangente
La cotangente de un ángulo en el círculo unitario se define como el cociente entre el coseno y el seno de ese ángulo.
Otras funciones trigonométricas, como la secante y la cosecante, se derivan a partir de estas funciones básicas.
El círculo unitario es una herramienta poderosa para comprender y calcular las funciones trigonométricas, y se utiliza ampliamente en diversos campos de la ciencia y la ingeniería.
4. El círculo general y sus funciones trigonométricas
En trigonometría, el círculo general es una figura geométrica que se utiliza para representar las relaciones entre los ángulos y las razones trigonométricas. Es un círculo de radio unitario, es decir, de radio 1, con el centro en el origen de un sistema de coordenadas cartesianas.
Las funciones trigonométricas son las razones entre las longitudes de dos lados en un triángulo rectángulo, y pueden ser representadas utilizando el círculo general. Las funciones trigonométricas más comunes son:
- Seno (sin): La función seno está definida como la longitud del cateto opuesto dividida por la hipotenusa de un triángulo rectángulo.
- Coseno (cos): La función coseno está definida como la longitud del cateto adyacente dividida por la hipotenusa de un triángulo rectángulo.
- Tangente (tan): La función tangente está definida como la longitud del cateto opuesto dividida por la longitud del cateto adyacente de un triángulo rectángulo.
Estas funciones son fundamentales en trigonometría y tienen numerosas aplicaciones en matemáticas, física, ingeniería y otras disciplinas científicas.
Además de estas funciones trigonométricas básicas, existen otras funciones trigonométricas como el secante, cosecante y cotangente, las cuales son el reciprocals de las funciones seno, coseno y tangente, respectivamente.
En resumen, el círculo general y las funciones trigonométricas son herramientas esenciales en trigonometría para representar y calcular relaciones angulares. Estas funciones tienen una amplia gama de aplicaciones en diferentes campos de estudio y son fundamentales para comprender diversos fenómenos naturales y científicos.
5. Aplicaciones de las funciones trigonométricas en el círculo unitario y general
En matemáticas, las funciones trigonométricas tienen numerosas aplicaciones, especialmente en el estudio de los círculos y las proporciones entre sus elementos. Estas funciones son especialmente útiles cuando se considera el círculo unitario, que es un círculo con un radio de 1 unidad y centrado en el origen de un sistema de coordenadas.
Una de las aplicaciones más comunes de las funciones trigonométricas en el círculo unitario es la representación de puntos en el plano cartesiano. Al considerar un punto en el círculo unitario, su posición se puede describir mediante el ángulo que forma con el eje x positivo. Esto se logra utilizando las funciones trigonométricas seno y coseno.
El seno de un ángulo en el círculo unitario se define como la coordenada y del punto en el círculo unitario que forma ese ángulo con el eje x positivo. Por otro lado, el coseno de un ángulo se define como la coordenada x del punto en el círculo unitario que forma ese ángulo con el eje x positivo. Ambas funciones son fundamentales para determinar la ubicación de un punto en el círculo unitario y, por lo tanto, tienen aplicaciones importantes en campos como la física y la ingeniería.
Además de las aplicaciones en el círculo unitario, las funciones trigonométricas también se utilizan en el estudio de triángulos generales. Por ejemplo, al resolver triángulos rectángulos, las funciones trigonométricas seno, coseno y tangente son esenciales para determinar las longitudes de los lados o los valores de los ángulos.
En resumen, las funciones trigonométricas tienen una amplia variedad de aplicaciones en el círculo unitario y en el estudio de triángulos generales. Su uso en la representación de puntos en el círculo unitario y en la resolución de triángulos permite resolver problemas complejos relacionados con el espacio y las proporciones de las figuras geométricas. Estas aplicaciones juegan un papel crucial en campos como la física, la ingeniería y la navegación.