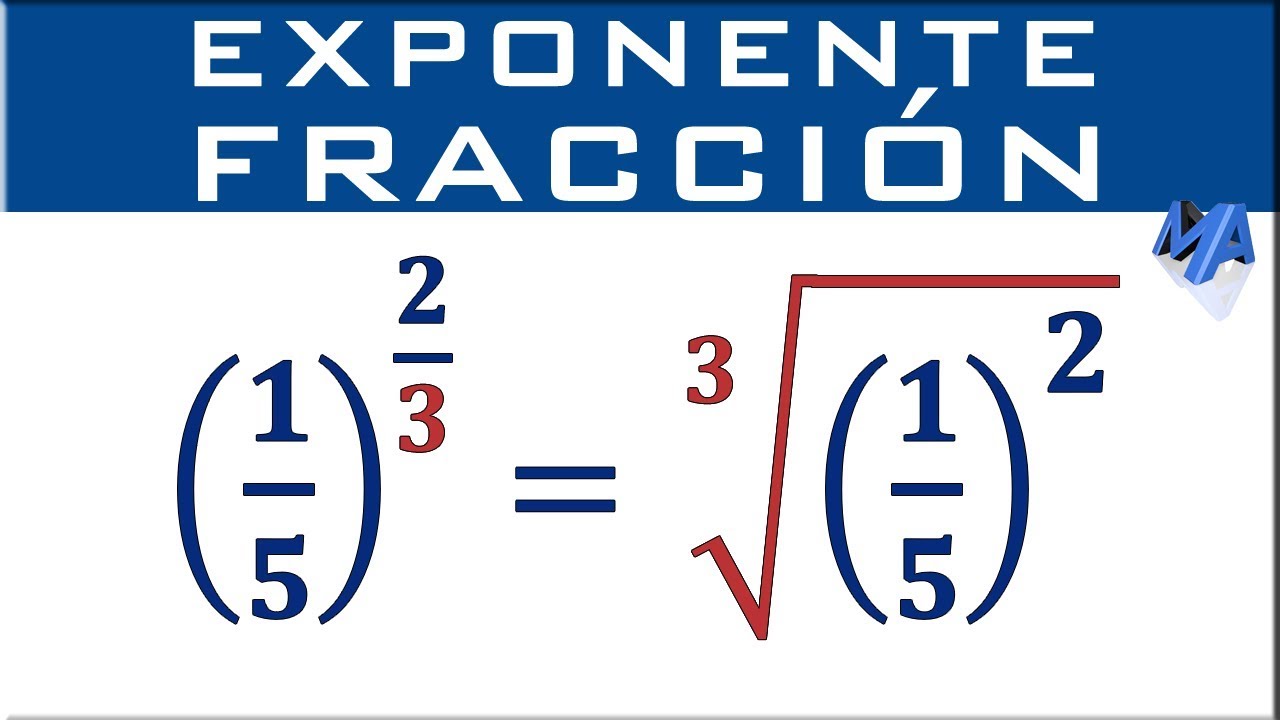
Qué son los exponentes racionales
El concepto de exponentes racionales se refiere a la potenciación de un número utilizando fracciones como exponente. Esto significa que en lugar de tener un número entero como exponente, se utiliza una fracción que representa una razón o proporción.
Por ejemplo, si tenemos el número 2 elevado a la potencia 1/2, esto significa que estamos calculando la raíz cuadrada de 2. El resultado sería √2, que es una aproximación de 1.414.
Los exponentes racionales también se pueden utilizar para calcular raíces cúbicas, cuartas, quintas, etc. Por ejemplo, si tenemos el número 8 elevado a la potencia 1/3, estamos calculando la raíz cúbica de 8, que es igual a 2.
Es importante destacar que los exponentes racionales también pueden ser negativos. En este caso, indican que debemos calcular la inversa de la potencia. Por ejemplo, si tenemos el número 4 elevado a la potencia -1/2, esto significa que debemos calcular la inversa de la raíz cuadrada de 4, que es igual a 1/√4, o 1/2.
En resumen, los exponentes racionales son una manera de calcular potencias utilizando fracciones como exponente. Permiten calcular raíces y expresar proporciones de una manera más precisa.
Exponentes mixtos en números enteros
El concepto de exponentes mixtos en números enteros es una combinación de dos conceptos matemáticos fundamentales: exponentes y números enteros.
Los exponentes son una forma de abreviar la multiplicación de un número por sí mismo varias veces. Por ejemplo, 2 al exponente 3 (2³) significa multiplicar 2 por sí mismo 3 veces, lo que resulta en 2 x 2 x 2 = 8.
Los números enteros, por otro lado, son números positivos o negativos sin fracciones ni decimales. Ejemplos de números enteros son -3, 0 y 7.
Cuando se combinan exponentes y números enteros, podemos tener exponentes mixtos en números enteros. Un exponente mixto en un número entero es cuando el exponente es un número entero positivo o negativo. Por ejemplo, 2 al exponente -3 (2⁻³) significa tomar el recíproco de 2 al exponente 3, es decir, 1 / (2³) = 1 / (2 x 2 x 2) = 1 / 8 = 0.125.
Los exponentes mixtos en números enteros también pueden aparecer en problemas matemáticos más complejos, donde se combinan operaciones como suma, resta, multiplicación o división con exponentes. En estos casos, es importante seguir las reglas matemáticas adecuadas para evaluar correctamente la expresión.
En conclusión, los exponentes mixtos en números enteros son una combinación de los conceptos de exponentes y números enteros. Permiten abreviar operaciones de multiplicación o división y pueden aparecer en problemas matemáticos más complejos. Es esencial comprender las reglas matemáticas correspondientes para resolver correctamente estas expresiones.
Exponentes mixtos en números decimales
Los exponentes mixtos en números decimales son una forma de representar números que incluyen tanto la parte entera como la fracción decimal, elevados a una potencia. Estos exponentes se utilizan para simplificar la escritura de números muy grandes o muy pequeños.
Por ejemplo, el número 102.5 podría escribirse como 102 * 100.5, lo cual significa que se multiplica 10 por sí mismo dos veces y luego se multiplica por la raíz cuadrada de 10.
Usar exponentes mixtos en números decimales puede hacer que las operaciones matemáticas sean más sencillas y fáciles de entender. También ayuda a reducir el número de ceros y facilita la comunicación de números complejos.
Ejemplos
A continuación, se presentan algunos ejemplos de exponentes mixtos en números decimales:
- 21.5 = 2 * √2
- 100.3 = 10 * ∛10
- 32.25 = 32 * √3
En estos ejemplos, la parte entera del exponente indica la cantidad de veces que se multiplica el número por sí mismo, mientras que la parte decimal indica la raíz cuadrada, cúbica, etc., del número.
Es importante tener en cuenta que los exponentes mixtos en números decimales solo se utilizan en casos específicos y no son comunes en todas las operaciones matemáticas.
Exponentes mixtos en números fraccionarios
Existen situaciones en las que nos encontramos con exponentes mixtos al trabajar con números fraccionarios. Un exponente mixto se refiere a una fracción en la que tanto el numerador como el denominador son números enteros, pero uno de ellos es negativo.
En matemáticas, cuando tenemos el exponente de un número fraccionario, podemos interpretarlo como una forma de indicar cuantas veces se debe multiplicar esa fracción por sí misma. Por ejemplo, si tenemos la fracción 2/3 y el exponente 2, significa que debemos multiplicar 2/3 por sí misma dos veces.
Para calcular el resultado, elevamos tanto el numerador como el denominador a la potencia indicada por el exponente. En este ejemplo, el cálculo sería:
(2/3)^2 = (2^2)/(3^2) = 4/9
En el caso de exponentes mixtos, donde uno de los términos es negativo, seguimos el mismo proceso. Sin embargo, antes de elevar a la potencia indicada, debemos tomar en cuenta que el exponente negativo implica invertir la fracción.
Veamos un ejemplo: si tenemos la fracción 3/4 elevada al exponente -2, el cálculo sería:
(3/4)^-2 = (4/3)^2 = (4^2)/(3^2) = 16/9
Como podemos observar, al invertir la fracción antes de elevarla a la potencia, obtenemos un resultado distinto al de un exponente positivo.
Es importante tener en cuenta estas reglas al trabajar con exponentes mixtos en números fraccionarios. De esta manera, podremos realizar cálculos precisos y obtener los resultados correctos.
Propiedades de los exponentes racionales
Los exponentes racionales son aquellos en los que el exponente es un número fraccionario. Estas propiedades son útiles para simplificar y operar con expresiones algebraicas que tienen exponentes racionales.
1. Regla de base elevada a un exponente racional: Si tenemos una base elevada a un exponente racional, podemos expresarla como una raíz. Por ejemplo, si tenemos a^m/n, donde m y n son números enteros y n es diferente de cero, podemos escribirlo como la raíz n-ésima de a elevado a la potencia m.
2. Regla de multiplicación de exponentes racionales: Si tenemos una base común elevada a dos exponentes racionales, podemos multiplicar los exponentes. Por ejemplo, si tenemos a^m/n * a^p/q, donde m, n, p y q son números enteros y n y q son diferentes de cero, podemos escribirlo como a^(mq/nq+mp/nq).
3. Regla de división de exponentes racionales: Si tenemos una fracción de dos bases comunes elevadas a exponentes racionales, podemos restar los exponentes. Por ejemplo, si tenemos (a^m/n)/(a^p/q), donde m, n, p y q son números enteros y n y q son diferentes de cero, podemos escribirlo como a^(mq/nq-mp/nq).
4. Regla de potencia de exponente racional: Si tenemos una base elevada a un exponente racional, y este exponente se encuentra elevado a su vez a otro exponente racional, podemos multiplicar los exponentes. Por ejemplo, si tenemos (a^m/n)^p/q, donde m, n, p y q son números enteros y n y q son diferentes de cero, podemos escribirlo como a^(mp/nq).
Estas son algunas de las propiedades más importantes de los exponentes racionales. Con estas reglas, podemos simplificar y operar con expresiones algebraicas de manera más sencilla y eficiente.