«`html
Las funciones trigonométricas son fundamentales en el campo de las matemáticas y tienen aplicaciones en diversos campos, desde la física hasta la ingeniería. En este artículo, exploraremos en profundidad dos de las funciones trigonométricas más importantes: el seno y el coseno.
«`
«`html
La importancia del seno y coseno en trigonometría
«`
La trigonometría es una rama crucial de las matemáticas que se centra en el estudio de las relaciones entre los ángulos y los lados de los triángulos. El seno y el coseno son dos de las funciones trigonométricas más esenciales, y su comprensión es fundamental para resolver problemas geométricos y aplicar conceptos matemáticos en situaciones del mundo real. Estas funciones tienen una amplia gama de aplicaciones en campos como la navegación, la ingeniería, la física, la arquitectura, la astronomía y mucho más. Comprender a fondo el comportamiento del seno y el coseno es crucial para los profesionales que trabajan en estas disciplinas, así como para los estudiantes que buscan desarrollar una base sólida en matemáticas y ciencias.
¿Qué es el seno?
El seno es una función trigonométrica que se define como la razón entre el lado opuesto a un ángulo en un triángulo rectángulo y la longitud de la hipotenusa. En otras palabras, para un ángulo θ, el seno se calcula como la longitud del lado opuesto dividido por la longitud de la hipotenusa. Esta relación es fundamental en la trigonometría y permite modelar una amplia gama de fenómenos naturales y artificiales.
Relación del seno con el ciclo trigonométrico
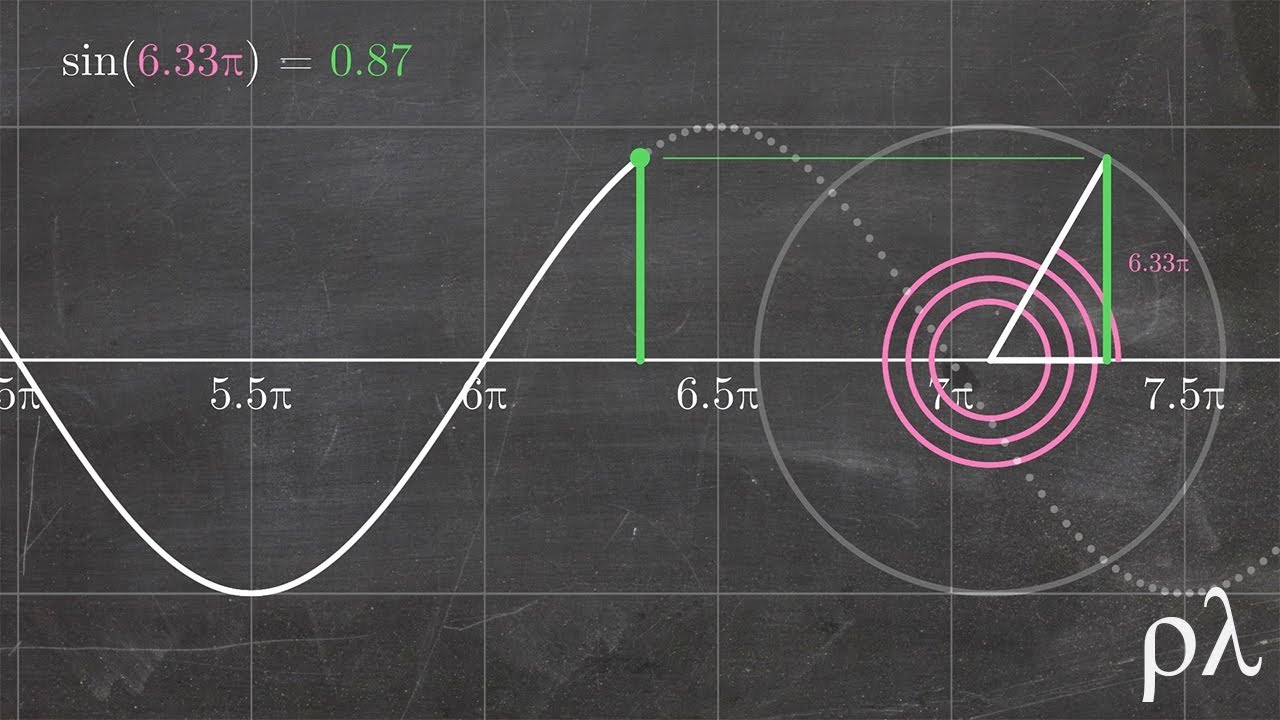
En el ciclo trigonométrico, el seno representa la altura de un punto en la circunferencia unitaria. Conforme el ángulo varía de 0 a 360 grados (o de 0 a 2π radianes), el valor del seno oscila entre -1 y 1, generando una forma de onda sinusoidal que es fundamental para modelar fenómenos periódicos como el movimiento armónico simple, las ondas sonoras y electromagnéticas, entre otros.
Representación gráfica del seno
Cuando se grafica el seno en función del ángulo, se obtiene una curva sinusoidal que oscila entre -1 y 1. Esta representación gráfica es crucial para visualizar y comprender el comportamiento del seno en un rango específico de ángulos. La periodicidad y la amplitud de la curva senoidal son conceptos fundamentales que describen el comportamiento del seno en el contexto de fenómenos periódicos.
¿Qué es el coseno?
El coseno es otra función trigonométrica esencial que está estrechamente relacionada con el seno. Se define como la razón entre el lado adyacente a un ángulo en un triángulo rectángulo y la longitud de la hipotenusa. En términos simples, para un ángulo θ, el coseno se calcula como la longitud del lado adyacente dividido por la longitud de la hipotenusa. Al igual que el seno, el coseno juega un papel crucial en la resolución de problemas geométricos y en la modelación de diversos fenómenos naturales y físicos.
Relación del coseno con el ciclo trigonométrico
En el ciclo trigonométrico, el coseno representa la abscisa de un punto en la circunferencia unitaria. Al igual que el seno, el valor del coseno oscila entre -1 y 1 a medida que el ángulo varía en el rango de 0 a 360 grados (o 0 a 2π radianes). La representación gráfica del coseno también es una curva sinusoidal, pero desplazada en fase con respecto al seno, lo que resulta en un comportamiento distintivo con respecto a la variación del ángulo.
Interrelación entre seno y coseno
El seno y el coseno están estrechamente relacionados entre sí, y esta relación es fundamental en el estudio de las funciones trigonométricas. De hecho, el coseno de un ángulo es igual al seno del complemento de ese ángulo, lo que establece una conexión directa entre estas dos funciones. Esta interrelación juega un papel crucial en la simplificación de expresiones trigonométricas y en la resolución de problemas geométricos y físicos.
Aplicaciones del seno y coseno
El seno y el coseno tienen una amplia gama de aplicaciones prácticas en diversos campos.
Aplicaciones en física y ingeniería
En física, el seno y el coseno se utilizan para modelar fenómenos como el movimiento armónico simple, las ondas sonoras, electromagnéticas y el comportamiento oscilatorio de sistemas físicos. En ingeniería, estas funciones tienen aplicaciones en la construcción de estructuras, el diseño de circuitos electrónicos y la análisis de sistemas mecánicos, entre otros.
El seno y el coseno son fundamentales en la navegación marítima y aérea, ya que se utilizan para calcular distancias y direcciones. En cartografía, estas funciones son esenciales para representar la forma y el tamaño de la Tierra en mapas y sistemas de posicionamiento global.
Aplicaciones en ciencias naturales
En disciplinas como la astronomía y la geología, el seno y el coseno se utilizan para modelar fenómenos astronómicos, como el movimiento aparente de los cuerpos celestes, y para analizar la geometría de formaciones geológicas.
En resumen, las funciones trigonométricas del seno y el coseno desempeñan un papel fundamental en el estudio y la aplicación de conceptos matemáticos en diversos campos. La comprensión de estas funciones esencialmente enriquece nuestra capacidad para modelar y comprender fenómenos naturales y físicos, así como para resolver problemas geométricos y analíticos de manera efectiva._GenericClass_