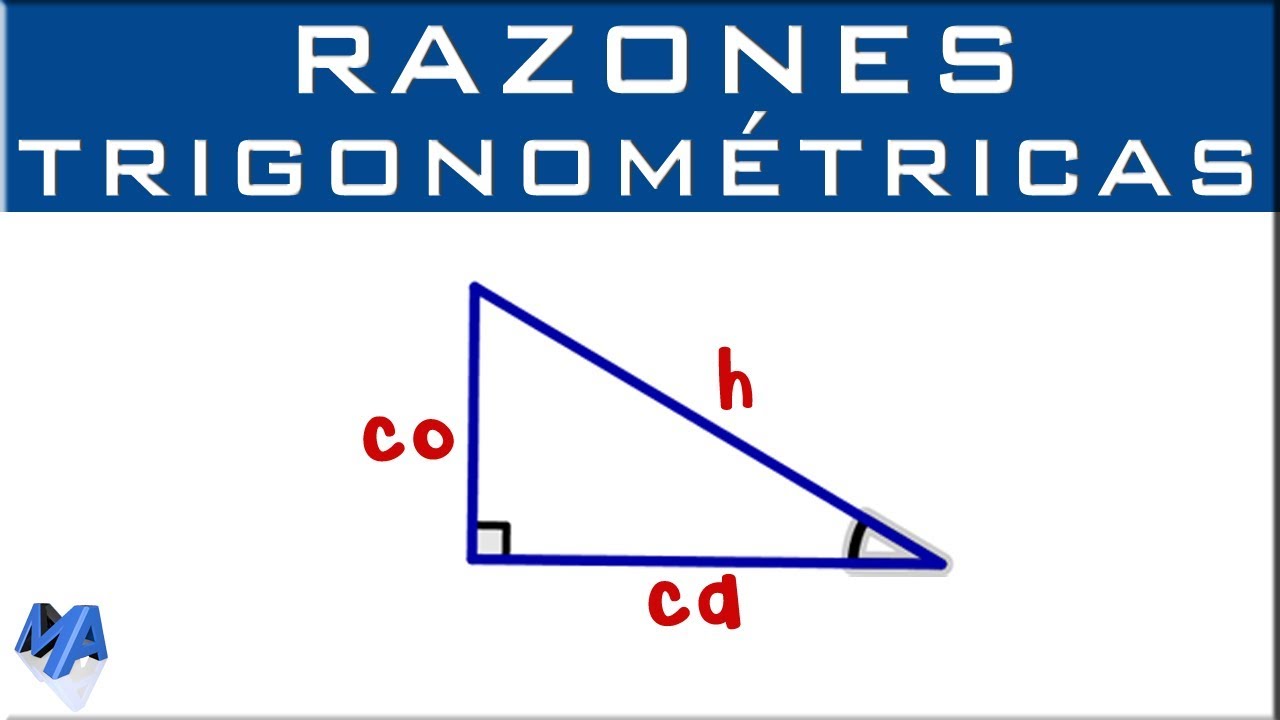
Concepto de Razón Trigonométrica en Triángulos Rectángulos
En el ámbito de la trigonometría, la relación entre los lados de un triángulo rectángulo y los ángulos internos es fundamental. Específicamente, la fórmula que expresa la razón entre el cateto opuesto y el cateto adyacente, es de suma importancia en diversos cálculos trigonométricos. En este artículo exploraremos detalladamente esta fórmula, su aplicación y su relevancia en el campo de las matemáticas y la geometría.
Definición y Nomenclatura
Cuando nos referimos a la razón entre el cateto opuesto y el cateto adyacente en un triángulo rectángulo, estamos hablando de la relación trigonométrica conocida como tangente, representada por la función tg o tan. Para comprender esta relación, es esencial tener claro el significado de los términos involucrados. El cateto opuesto se refiere al lado del triángulo que está enfrentado al ángulo en cuestión, mientras que el cateto adyacente es el lado que se encuentra contiguo a dicho ángulo.
La Fórmula de la Tangente
La fórmula que expresa la tangente de un ángulo θ en un triángulo rectángulo se define como la razón entre el cateto opuesto y el cateto adyacente. Matemáticamente, esto se expresa como:
[ tan(θ) = frac{{text{{Cateto Opuesto}}}}{{text{{Cateto Adyacente}}} } ]
Esta fórmula es fundamental para realizar cálculos relacionados con triángulos rectángulos, así como en aplicaciones más avanzadas en trigonometría y geometría analítica.
Aplicaciones en la Resolución de Problemas
La fórmula de la tangente encuentra una amplia variedad de aplicaciones en la resolución de problemas prácticos. Por ejemplo, en arquitectura e ingeniería civil, el cálculo de ángulos y distancias en estructuras es esencial para el diseño y la construcción de edificaciones. La fórmula de la tangente permite a los profesionales de estas áreas realizar cálculos precisos que garantizan la estabilidad y seguridad de las estructuras.
En el campo de la navegación marítima, aérea y terrestre, la trigonometría es fundamental para determinar la posición y el rumbo de vehículos y embarcaciones. La fórmula de la tangente se utiliza en cálculos de triangulación y en la interpretación de coordenadas geográficas, contribuyendo a la seguridad y precisión de las operaciones de navegación.
Aplicaciones en el Desarrollo de Software
La trigonometría, incluida la fórmula de la razón entre el cateto opuesto y el cateto adyacente, también desempeña un papel crucial en el desarrollo de software. En campos como la animación por computadora, los videojuegos y la simulación de fenómenos físicos, las funciones trigonométricas son utilizadas para calcular posiciones, movimientos y efectos visuales de forma precisa y realista.
Relación con Otras Funciones Trigonométricas
La fórmula de la tangente está estrechamente relacionada con otras funciones trigonométricas, como el seno y el coseno. Estas funciones son fundamentales en trigonometría y están intrínsecamente conectadas a través de identidades trigonométricas, lo que permite realizar diversas transformaciones y simplificaciones en cálculos trigonométricos.
Identidades Trigonométricas Básicas
Las identidades trigonométricas son ecuaciones que relacionan las funciones trigonométricas entre sí. Algunas de las identidades básicas relacionadas con la fórmula de la tangente son:
[ tan(θ) = frac{{sin(θ)}}{{cos(θ)}} ]
[ sin^2(θ) + cos^2(θ) = 1 ]
Estas identidades son esenciales para simplificar expresiones trigonométricas, resolver ecuaciones y realizar transformaciones entre funciones trigonométricas.
Aplicación en la Resolución de Ecuaciones Trigonométricas
La relación entre la tangente, el seno y el coseno es fundamental al resolver ecuaciones trigonométricas. Al aplicar identidades trigonométricas y manipular las funciones, es posible simplificar ecuaciones complejas y encontrar soluciones exactas para diversos problemas matemáticos y físicos.
Desarrollo Histórico y Significado Cultural
El estudio de las funciones trigonométricas, incluida la fórmula de la tangente, tiene profundas raíces históricas y culturales. Estas funciones han sido estudiadas y utilizadas a lo largo de la historia en diversas civilizaciones, desde la antigua Grecia hasta las contribuciones posteriores de matemáticos árabes, hindúes y europeos.
La importancia de la trigonometría y sus funciones en campos como la astronomía y la navegación ha sido crucial para el desarrollo de la ciencia y la exploración. Antiguamente, la medición de ángulos celestiales y la determinación de posiciones geográficas dependían en gran medida de cálculos trigonométricos, incluida la fórmula de la tangente.
Influencia en el Arte y la Arquitectura
La aplicación de principios trigonométricos en la representación visual y la construcción arquitectónica ha influido en numerosas expresiones artísticas y arquitectónicas a lo largo de la historia. Desde la antigüedad hasta la era moderna, el entendimiento de las relaciones espaciales y angulares ha sido fundamental en la creación de obras de arte y monumentos arquitectónicos icónicos.
Avances Contemporáneos y Futuras Aplicaciones
En la actualidad, el uso de la fórmula de la tangente y otras funciones trigonométricas se extiende a campos innovadores como la astronomía computacional, la robótica y la visualización de datos en tiempo real. Estos avances abren nuevas posibilidades para la aplicación de la trigonometría en contextos tecnológicos de vanguardia, contribuyendo a la evolución de la ciencia y la ingeniería.
Trigonometría en la Ciencia de Datos
La trigonometría juega un papel crucial en el análisis y la visualización de datos en el campo de la ciencia de datos. La aplicación de funciones trigonométricas permite modelar y comprender fenómenos periódicos, así como analizar datos que exhiben comportamientos cíclicos, como las fluctuaciones estacionales o las oscilaciones de señales electromagnéticas.
Integración en la Inteligencia Artificial y la Automatización
En el contexto de la inteligencia artificial y la automatización, la trigonometría, incluida la fórmula de la tangente, es utilizada para desarrollar algoritmos y sistemas que requieren comprender y procesar datos espaciales, temporales y angulares de forma eficiente y precisa.
En resumen, la fórmula de la razón entre el cateto opuesto y el cateto adyacente, conocida como tangente, desempeña un papel fundamental en numerosos campos de la ciencia, la ingeniería, las matemáticas aplicadas y la tecnología. Su relevancia histórica, su aplicación práctica y su integración en avances contemporáneos demuestran la importancia continua de la trigonometría en la comprensión y la manipulación de fenómenos angulares y espaciales en el mundo actual.