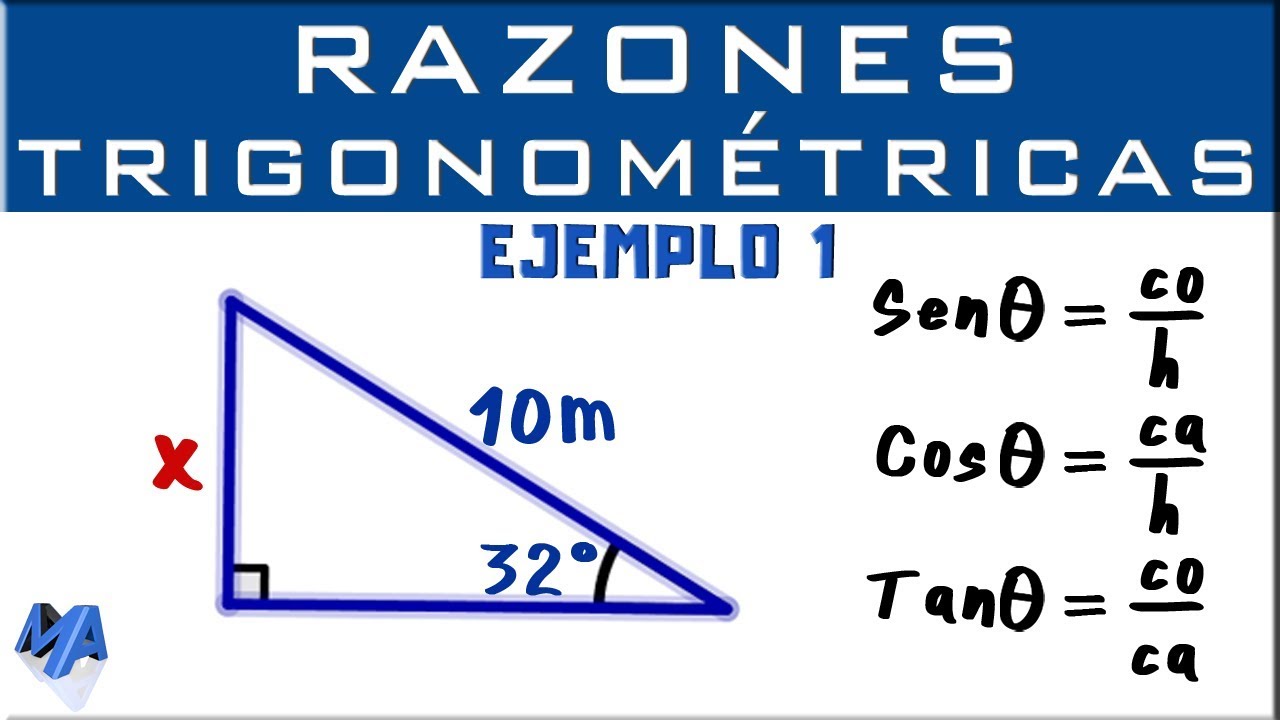
La trigonometría es una rama de las matemáticas que se ocupa de los ángulos y de las relaciones entre los lados de triángulos. En trigonometría, una de las razones trigonométricas fundamentales es la tangente, que se define como la relación entre el cateto opuesto y el cateto adyacente a un ángulo en un triángulo rectángulo. Calcular la tangente de un ángulo es fundamental en muchas aplicaciones de la trigonometría, y una forma de hacerlo es mediante la división de catetos.
Demostración de la fórmula
Para calcular la tangente de un ángulo en un triángulo rectángulo, se puede utilizar la fórmula matemática que relaciona la tangente con la división de catetos. Esta fórmula se basa en la definición misma de la tangente y es fundamental para comprender y aplicar la trigonometría en problemas reales y teóricos.
Definición de la tangente
Antes de derivar la fórmula para calcular la tangente mediante la división de catetos, es importante recordar la definición de la tangente. En un triángulo rectángulo, la tangente del ángulo agudo θ se define como la razón entre el cateto opuesto (O) y el cateto adyacente (A), es decir, tan(θ) = O/A. Esta definición es fundamental para comprender el concepto de la tangente y su relación con los catetos del triángulo.
Fórmula de la tangente
La fórmula para calcular la tangente mediante la división de catetos surge directamente de la definición de la tangente y la relación entre los lados de un triángulo rectángulo. La fórmula se expresa como tan(θ) = O/A, donde θ es el ángulo agudo, O es la longitud del cateto opuesto y A es la longitud del cateto adyacente al ángulo θ. Al utilizar esta fórmula, es posible calcular la tangente de un ángulo concreto en un triángulo rectángulo con precisión y facilidad.
Aplicaciones de la fórmula en problemas prácticos
La fórmula para calcular la tangente mediante la división de catetos tiene numerosas aplicaciones en problemas prácticos. Desde la resolución de triángulos hasta la determinación de ángulos en situaciones cotidianas, comprender y aplicar esta fórmula es esencial para los estudiantes de trigonometría y para profesionales que utilizan conceptos matemáticos en su trabajo.
Resolución de triángulos
Una de las aplicaciones más comunes de la fórmula de la tangente es la resolución de triángulos. Dado un triángulo rectángulo con dos lados conocidos, es posible utilizar la fórmula para calcular la tangente y, a partir de ahí, determinar el valor de un ángulo desconocido. Esta aplicación es fundamental en la resolución de problemas geométricos y de ingeniería que involucran triángulos rectángulos.
Estimación de alturas y distancias
Otra aplicación práctica de la fórmula de la tangente es la estimación de alturas y distancias. Por ejemplo, en topografía y cartografía, es posible utilizar la tangente para determinar la altura de un edificio o la distancia a un objeto, simplemente midiendo ángulos y longitudes de catetos. Esta aplicación demuestra la utilidad real de la trigonometría en situaciones cotidianas.
Consideraciones especiales
A pesar de su utilidad, es importante tener en cuenta algunas consideraciones especiales al utilizar la fórmula para calcular la tangente mediante la división de catetos. Estas consideraciones permiten evitar errores y comprender mejor la aplicación de esta fórmula en diferentes contextos matemáticos y físicos.
Restricciones del dominio
Es fundamental recordar las restricciones del dominio al utilizar la fórmula de la tangente en trigonometría. En particular, la tangente posee asintotas verticales en los ángulos donde el cateto adyacente es igual a cero, lo que resulta en valores no definidos para la tangente. Estas restricciones deben considerarse al aplicar la fórmula en diferentes contextos matemáticos y físicos.
Precisión y redondeo
Otra consideración importante es la precisión y el redondeo al utilizar la fórmula de la tangente. En situaciones prácticas, es necesario considerar la precisión de las medidas de los catetos y los ángulos, así como el redondeo adecuado de los resultados para evitar errores significativos en los cálculos. La precisión es crucial para obtener resultados fiables y útiles en aplicaciones reales.
En resumen, la fórmula para calcular la tangente mediante la división de catetos es fundamental en la trigonometría, con numerosas aplicaciones en problemas teóricos y prácticos. Comprender esta fórmula y sus aplicaciones es esencial para estudiantes y profesionales que trabajan con conceptos trigonométricos en diversos campos. Al dominar esta fórmula y sus consideraciones especiales, es posible utilizar la trigonometría de manera efectiva y precisa en una amplia gama de situaciones.
¿Te ha resultado útil este contenido? ¡Comparte estos conocimientos con tus compañeros y amigos!