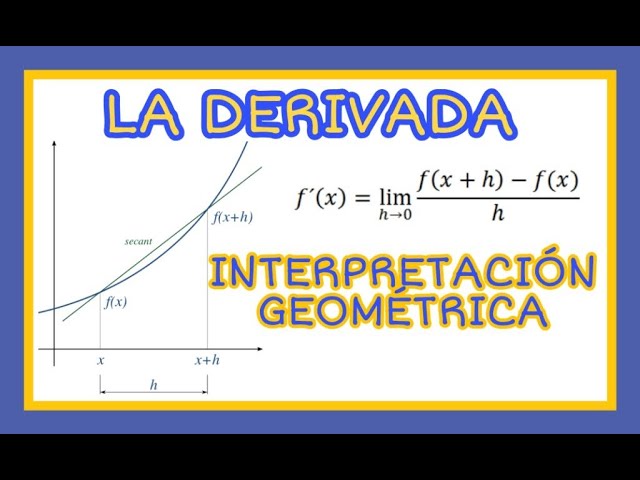
La interpretación geométrica de la derivada de una función es un concepto fundamental en el cálculo y la matemática en general. La derivada de una función en un punto dado proporciona información sobre la pendiente de la recta tangente a la curva en ese punto, lo que tiene importantes implicaciones geométricas y físicas. Exploraremos en detalle esta interpretación y su relevancia en diversos contextos.
El concepto de derivada
Antes de sumergirnos en la interpretación geométrica de la derivada, es crucial tener una comprensión clara del concepto de derivada en sí. La derivada de una función en un punto específico representa la tasa de cambio instantánea de la función en ese punto. En otras palabras, nos dice cómo está cambiando la función en un punto dado. Este concepto es fundamental en el análisis matemático y tiene numerosas aplicaciones en física, economía, ingeniería y otras disciplinas.
La recta tangente
Una vez que entendemos la noción de derivada, podemos adentrarnos en su interpretación geométrica. La derivada de una función en un punto dado nos proporciona la pendiente de la recta tangente a la curva de la función en ese punto. Esta recta tangente es crucial para comprender el comportamiento local de la función y es fundamental para visualizar su variación en un punto específico.
Pendiente de la recta tangente
La pendiente de la recta tangente a la curva en un punto dado es igual a la derivada de la función en ese punto. Esta relación es esencial para la comprensión geométrica de la derivada. Visualmente, la pendiente de la recta tangente representa la inclinación de la curva en ese punto, lo que nos brinda información valiosa sobre cómo la función cambia en su entorno más inmediato.
Interpretación física
En el contexto físico, la interpretación geométrica de la derivada es fundamental para comprender conceptos como velocidad y aceleración. La derivada de la posición de un objeto con respecto al tiempo nos brinda la velocidad instantánea del objeto en un momento dado. La idea de la recta tangente se traduce directamente en la noción de movimiento, donde la pendiente de la tangente representa la rapidez con la que el objeto se está desplazando en ese instante.
Curvatura de la función
Otro aspecto relevante de la interpretación geométrica de la derivada es su relación con la curvatura de la función. La segunda derivada de una función nos proporciona información sobre la curvatura de la curva en un punto dado. La curvatura está estrechamente relacionada con la forma en que la curva se dobla en su entorno, lo que tiene implicaciones significativas en diversos campos, como la física de partículas y la ingeniería estructural.
Aplicaciones en economía y finanzas
En el ámbito económico, la interpretación geométrica de la derivada es crucial para comprender la noción de cambio marginal. La derivada de una función que modela el costo o el ingreso de una empresa nos brinda información sobre cómo estos valores cambian en relación con la cantidad producida o vendida. La recta tangente a la curva de costo total, por ejemplo, nos brinda la tasa a la que el costo total está cambiando en un nivel de producción específico.
Conexiones con el cálculo integral
La interpretación geométrica de la derivada también está estrechamente relacionada con el cálculo integral. La noción de área bajo la curva, que es fundamental en el cálculo integral, tiene conexiones directas con la derivada y la recta tangente. La derivada nos brinda la pendiente de la tangente, mientras que el cálculo integral nos permite encontrar el área bajo la curva, lo que demuestra la profunda interconexión entre estos conceptos matemáticos.
Generalización a funciones multivariables
La interpretación geométrica de la derivada no se limita a funciones de una sola variable. En el caso de funciones multivariables, la derivada parcial nos brinda información sobre la tasa de cambio con respecto a cada una de las variables independientes. La idea de la recta tangente se generaliza a lo que se conoce como plano tangente, que es crucial para comprender la variación local de funciones de múltiples variables en el espacio.
Algoritmos de optimización
En el campo de la computación y el aprendizaje automático, la interpretación geométrica de la derivada juega un papel fundamental en los algoritmos de optimización. El cálculo de la derivada de una función de pérdida con respecto a los parámetros del modelo nos brinda información sobre cómo ajustar estos parámetros para minimizar la pérdida. La idea de la recta tangente se utiliza de manera fundamental en algoritmos como el descenso de gradiente para encontrar óptimos locales o globales en funciones de alta dimensionalidad.
En resumen, la interpretación geométrica de la derivada de una función es un concepto fundamental que tiene aplicaciones en una amplia gama de disciplinas, desde la física y la economía hasta la computación y la ingeniería. La comprensión de la relación entre la derivada y la recta tangente nos brinda una poderosa herramienta para visualizar y comprender el comportamiento de las funciones en diferentes contextos, lo que subraya su importancia tanto teórica como práctica en el estudio de las matemáticas y sus aplicaciones.