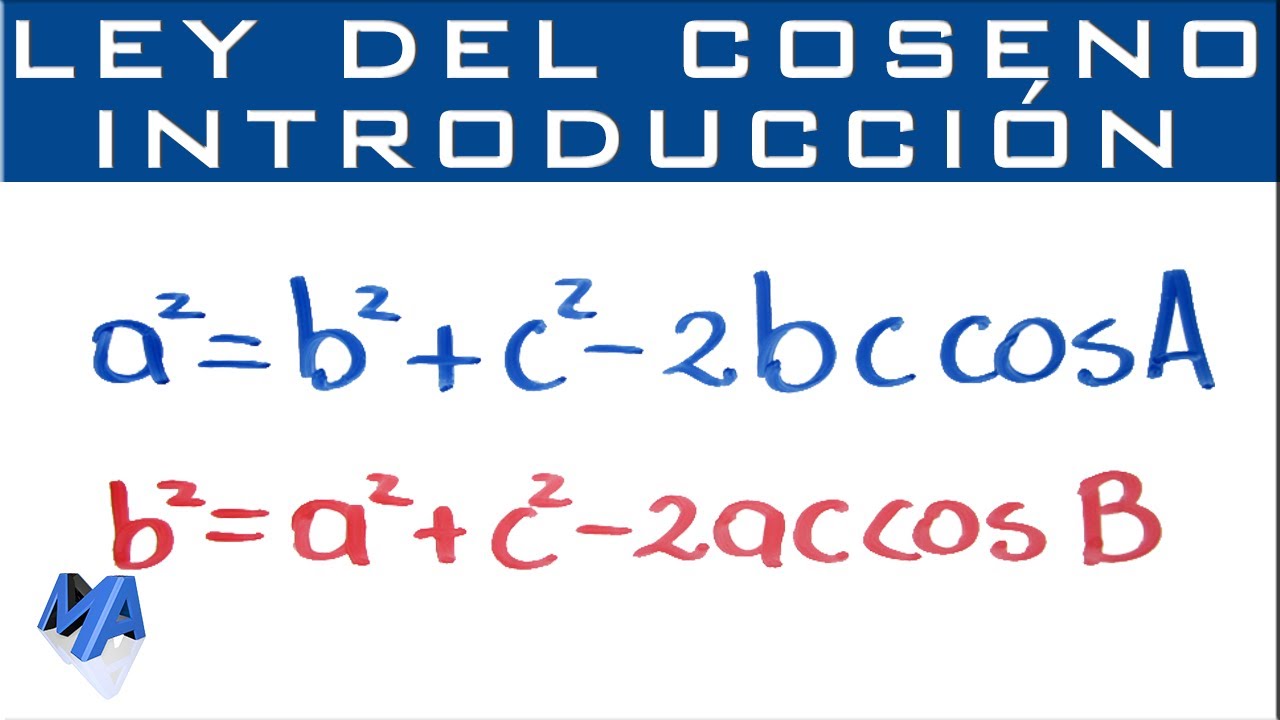Descifrando la ley de cosenos y su aplicación
La ley de cosenos es un concepto fundamental en trigonometría y geometría, que establece una relación entre los lados y ángulos de un triángulo. Esta ley es aplicable en una amplia gama de situaciones, desde la navegación marítima hasta la resolución de problemas geométricos. Sin embargo, su conexión con otros conceptos matemáticos puede no ser tan evidente a simple vista. En este artículo, exploraremos la relación deducible de la ley de cosenos con otros principios matemáticos, desentrañando su importancia y aplicaciones en diversas áreas.
El poder de la trigonometría en la resolución de problemas
La trigonometría es una rama de las matemáticas que se centra en las relaciones entre los ángulos y los lados de los triángulos. Su utilidad va más allá de los cálculos teóricos, ya que se aplica en campos tan diversos como la ingeniería, la física, la astronomía y la arquitectura. La ley de cosenos es una herramienta fundamental en trigonometría, ya que proporciona una forma de calcular la longitud de un lado de un triángulo cuando se conocen los otros lados y el ángulo entre ellos. Este poder para resolver problemas vinculados a la geometría y la medición lo convierte en un concepto invaluable en diversas disciplinas.
Conexiones sorprendentes: la relación con la fórmula de Pitágoras
La fórmula de Pitágoras es quizás una de las primeras relaciones matemáticas que aprendemos: en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados. Sin embargo, ¿cómo se relaciona esto con la ley de cosenos? La respuesta es que la ley de cosenos se convierte en la fórmula de Pitágoras cuando el triángulo en cuestión es un triángulo rectángulo, es decir, cuando el ángulo entre los dos lados es de 90 grados. Esta conexión revela una relación profunda entre dos conceptos aparentemente separados, demostrando la riqueza y la interconexión de las matemáticas.
Inmersión en la geodesia: aplicaciones en la medición de distancias en la Tierra
La geodesia es la ciencia que se ocupa de medir y representar la forma y el campo de gravedad de la Tierra. En este ámbito, la ley de cosenos es ampliamente utilizada para calcular distancias entre puntos en la superficie terrestre. Al emplear esta ley, los geodesistas pueden determinar con precisión la separación entre dos ubicaciones, teniendo en cuenta la curvatura de la Tierra. Además, la ley de cosenos se combina con otras herramientas matemáticas y tecnológicas para cartografiar el planeta, lo que impacta directamente en la navegación, la planificación de infraestructuras y la gestión de recursos naturales.
Abstracciones en el espacio: la geometría no euclidiana y la ley de cosenos
Mientras que la geometría euclidiana, basada en los postulados de Euclides, ha sido el enfoque principal en educación matemática durante siglos, la geometría no euclidiana ofrece un marco alternativo fascinante. En este contexto, la ley de cosenos adquiere una nueva relevancia al ser aplicada en geometrías no euclidianas, donde los postulados de Euclides son cuestionados. La relación deducible de la ley de cosenos con estos sistemas geométricos distintos proporciona una visión fascinante de cómo los principios matemáticos fundamentales pueden adaptarse a diferentes contextos, desafiando nuestras percepciones tradicionales del espacio y la forma.
La ley de cosenos tiene un impacto significativo en la determinación de posiciones en la esfera celeste, siendo crucial en campos como la astronomía y la navegación marítima. Cuando se observa la posición de astros o se traza una ruta en alta mar, la ley de cosenos entra en juego para calcular distancias y ángulos entre puntos de referencia. Esta aplicación práctica demuestra cómo un principio matemático aparentemente abstracto es fundamental para la comprensión y la navegación en el mundo real, conectando la teoría con la práctica de manera sorprendente.
Intersecciones con la física: trabajo, energía y la ley de cosenos
La relación deducible de la ley de cosenos con la física va más allá de la mera aplicación en cálculos geométricos. En el estudio del trabajo y la energía, la ley de cosenos es utilizada para descomponer fuerzas en componentes que actúan a lo largo y perpendicular a la dirección del movimiento. Este enfoque vectorial permite comprender cómo el trabajo y la energía se relacionan con las fuerzas aplicadas en distintas direcciones, proporcionando un fundamento matemático para abordar problemas de mecánica y dinámica. Así, la ley de cosenos se convierte en una herramienta fundamental en la modelización y análisis de sistemas físicos complejos.
La matemática detrás de la ingeniería estructural
Cuando se diseña una estructura, ya sea un puente, un edificio o una torre, es fundamental garantizar que soporte las fuerzas y cargas que actúan sobre ella. La ley de cosenos es esencial en la ingeniería estructural, ya que permite calcular las tensiones y compresiones resultantes de la distribución de fuerzas en los miembros de la estructura. Al comprender la relación entre las fuerzas y los ángulos en juego, los ingenieros pueden diseñar infraestructuras seguras y eficientes, aprovechando el poder de la ley de cosenos como una herramienta indispensable en el análisis estructural.
Una mirada al futuro: aplicaciones en tecnología y ciencia de datos
Con el avance de la tecnología y la creciente importancia de la ciencia de datos, la ley de cosenos encuentra nuevas aplicaciones innovadoras. En campos como la visión por computadora, el procesamiento de imágenes y la ingeniería de señales, esta ley es utilizada para calcular distancias y ángulos entre puntos en espacios multidimensionales, brindando herramientas cruciales para el análisis y la comprensión de datos complejos. Además, en el ámbito de la inteligencia artificial y el aprendizaje automático, la relación deducible de la ley de cosenos se manifiesta en algoritmos de clasificación y agrupamiento, revelando su influencia en el panorama tecnológico actual.
Impacto transcultural: la presencia de la ley de cosenos en la historia y el arte
Más allá de su utilidad en campos científicos y tecnológicos, la ley de cosenos ha dejado una huella en la cultura y la historia a lo largo de los siglos. En la arquitectura de antiguas civilizaciones, en las formas naturales y en las obras de arte, podemos encontrar manifestaciones de las relaciones geométricas que subyacen a la ley de cosenos. Estas conexiones entre la geometría y la expresión humana resaltan la relevancia perenne de los principios matemáticos, trascendiendo las barreras de tiempo y espacio para influir en la creatividad y la percepción humanas.
Explorando el potencial transformador: aplicación de la ley de cosenos en panoramas no convencionales
La versatilidad de la ley de cosenos se extiende más allá de los dominios convencionales de su aplicación. En disciplinas artísticas, como la música y la danza, los conceptos geométricos relacionados con la ley de cosenos han servido de inspiración para la creación de obras innovadoras. Del mismo modo, en el ámbito de la resolución de problemas complejos, la analogía matemática proporcionada por la ley de cosenos ha sido adoptada como un enfoque para abordar desafíos interdisciplinarios en campos tan diversos como la psicología, la economía y la sociología. Esta expansión hacia nuevos horizontes demuestra la capacidad transformadora de la ley de cosenos, que trasciende los límites tradicionales de su aplicación.
El camino hacia la comprensión: desafíos y reflexiones finales
A medida que exploramos las diversas facetas de la ley de cosenos y su relación con otros principios matemáticos, surge la complejidad y la riqueza de este concepto fundamental. Desde su interacción con la fórmula de Pitágoras hasta su influencia en la ingeniería y la tecnología, la ley de cosenos revela su omnipresencia y su poder para desbloquear nuevos entendimientos en contextos inesperados. Por lo tanto, al considerar la relación deducible de la ley de cosenos, nos enfrentamos a un desafío para mirar más allá de lo obvio y sumergirnos en la inmensidad del mundo matemático, donde cada conexión revela una perspectiva única y asombrosa.