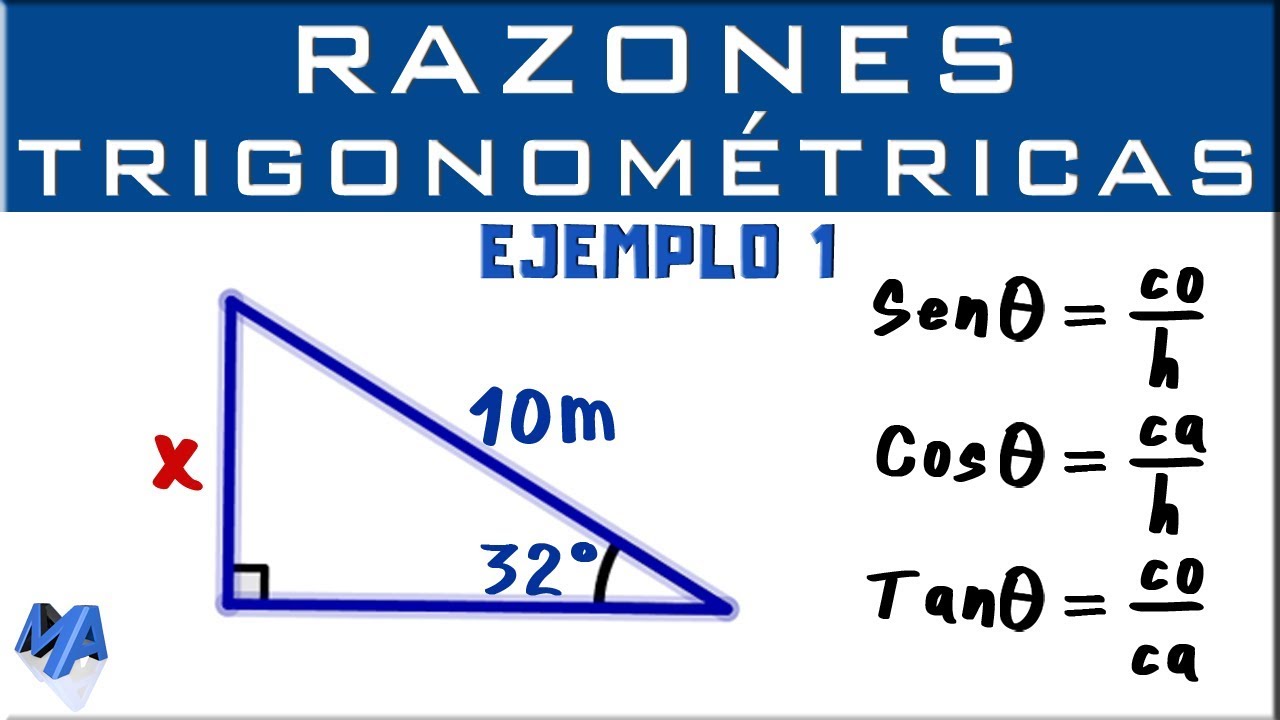
Descubriendo la razón trigonométrica
¿Alguna vez te has preguntado cómo obtener la razón trigonométrica al dividir la hipotenusa entre el cateto adyacente? La trigonometría es una rama fascinante de las matemáticas que estudia las relaciones entre los ángulos y los lados de un triángulo. En este artículo, vamos a explorar paso a paso cómo obtener esta importante razón trigonométrica y comprender su significado en el contexto de la geometría.
Conceptos básicos de trigonometría
Antes de sumergirnos en el cálculo de la razón trigonométrica, es importante entender algunos conceptos básicos. La trigonometría se enfoca en las propiedades y medidas de los triángulos, específicamente en relación con ángulos y longitudes de los lados. Los principales conceptos son el seno, el coseno y la tangente, que son funciones trigonométricas fundamentales y se derivan de las razones entre los lados de un triángulo rectángulo.
Triángulos rectángulos y sus elementos
Un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, un ángulo de 90 grados. Los elementos más importantes de un triángulo rectángulo son la hipotenusa y los catetos. La hipotenusa es el lado más largo, opuesto al ángulo recto, mientras que los catetos son los otros dos lados que forman el ángulo recto. En el contexto de la trigonometría, nos enfocaremos en la relación entre la hipotenusa y el cateto adyacente a un ángulo agudo.
Definición del coseno: adyacente sobre hipotenusa
El coseno de un ángulo en un triángulo rectángulo se define como la razón entre la longitud del cateto adyacente al ángulo y la longitud de la hipotenusa. Esta definición es fundamental para comprender la relación entre los ángulos y los lados de un triángulo rectángulo. Matemáticamente, el coseno se expresa como:
cos(θ) = cateto adyacente / hipotenusa
Cálculo de la razón trigonométrica
Ahora que hemos establecido la definición del coseno, podemos proceder a calcular la razón trigonométrica al dividir la hipotenusa entre el cateto adyacente. Este cálculo nos proporciona información valiosa sobre la relación entre los lados de un triángulo rectángulo y nos permite entender la geometría de manera más profunda.
Ejemplo de cálculo
Imagina un triángulo rectángulo con una hipotenusa de longitud 5 y un cateto adyacente de longitud 3. Para calcular la razón trigonométrica, simplemente dividimos la longitud de la hipotenusa entre la longitud del cateto adyacente:
razón trigonométrica = hipotenusa / cateto adyacente
En este caso, la razón trigonométrica sería:
razón trigonométrica = 5 / 3 = 1.67
Interpretación de la razón trigonométrica
Una vez que hemos calculado la razón trigonométrica, es importante entender su significado en el contexto del triángulo rectángulo. Esta razón nos proporciona información sobre la inclinación del triángulo y nos permite comparar las longitudes de la hipotenusa y el cateto adyacente en función del ángulo considerado.
Relación con el ángulo
La razón trigonométrica está estrechamente relacionada con el ángulo considerado en el triángulo rectángulo. A medida que el ángulo cambia, la razón trigonométrica también varía, lo que nos brinda información sobre cómo los lados del triángulo se relacionan en diferentes situaciones. Esta relación es fundamental en aplicaciones prácticas de la trigonometría, como la navegación, la ingeniería y la física.
Aplicaciones de la trigonometría
La trigonometría tiene numerosas aplicaciones en diversos campos, desde la construcción de edificios hasta la navegación marítima. Comprender la razón trigonométrica al dividir la hipotenusa entre el cateto adyacente nos permite resolver problemas reales y modelar situaciones del mundo real usando conceptos matemáticos fundamentales.
Ingeniería y arquitectura
En ingeniería y arquitectura, la trigonometría es esencial para calcular distancias, ángulos y dimensiones en estructuras y diseños. La razón trigonométrica es una herramienta invaluable para los profesionales que trabajan en estos campos, ya que les ayuda a realizar cálculos precisos y tomar decisiones fundamentadas sobre diseños y construcciones.
En la navegación y la cartografía, la trigonometría se utiliza para determinar la posición de un barco, avión o cualquier otro objeto en movimiento. La razón trigonométrica al dividir la hipotenusa entre el cateto adyacente es fundamental para calcular ángulos de dirección, medir distancias y trazar rutas de navegación seguras y eficientes.
En resumen, la obtención de la razón trigonométrica al dividir la hipotenusa entre el cateto adyacente es un concepto central en la trigonometría. A través de este artículo, hemos explorado los fundamentos de la trigonometría, comprendido la definición del coseno, calculado la razón trigonométrica y explorado sus aplicaciones en el mundo real. La trigonometría es una herramienta poderosa que tiene un impacto significativo en campos como la ingeniería, la arquitectura, la navegación y muchos otros aspectos de nuestra vida cotidiana.