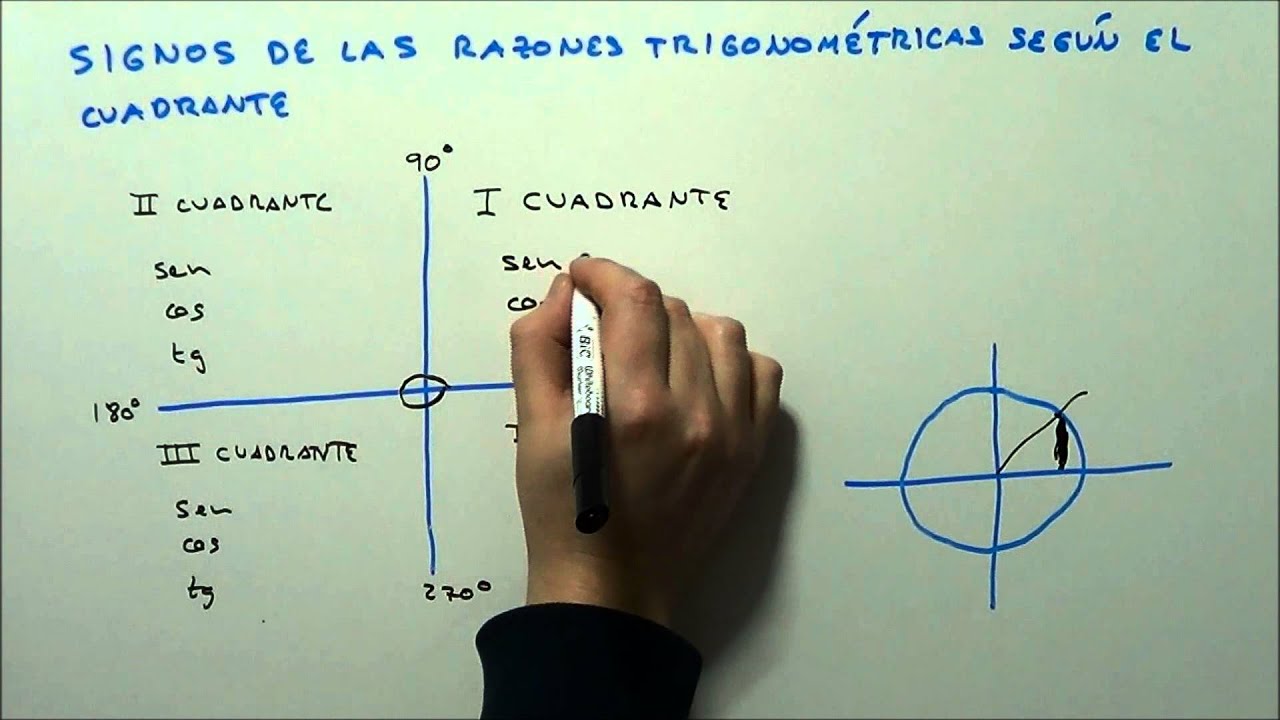
Las funciones trigonométricas son fundamentales en el estudio de las matemáticas y la física, y su comprensión es crucial para resolver una amplia gama de problemas. En particular, el tercer cuadrante del plano cartesiano juega un papel importante en el análisis de las funciones trigonométricas, ya que es en este cuadrante donde se encuentran los valores negativos de estas funciones.
¿Qué son las funciones trigonométricas?
Las funciones trigonométricas, como el seno, el coseno y la tangente, son herramientas matemáticas que describen las relaciones entre los ángulos y las longitudes de los lados de un triángulo. Estas funciones son cíclicas, lo que significa que sus valores se repiten a intervalos regulares.
El tercer cuadrante y los valores negativos
El tercer cuadrante del plano cartesiano se encuentra debajo del eje x y a la izquierda del eje y. En este cuadrante, tanto las coordenadas x como y son negativas, lo que tiene implicaciones significativas para las funciones trigonométricas.
El seno en el tercer cuadrante
El seno de un ángulo en el tercer cuadrante es negativo, ya que el valor y de las coordenadas en este cuadrante es negativo. Esto significa que el seno de un ángulo en el tercer cuadrante será negativo, lo que indica una dirección descendente desde el eje x.
El coseno en el tercer cuadrante
Similar al seno, el coseno de un ángulo en el tercer cuadrante también es negativo. Dado que el valor x de las coordenadas en este cuadrante es negativo, el coseno será negativo, indicando una dirección hacia la izquierda desde el eje y.
La tangente en el tercer cuadrante
En el tercer cuadrante, la tangente de un ángulo es positiva. Esto se debe a que la tangente se define como el cociente entre el seno y el coseno, y en este cuadrante ambos son negativos, resultando en una tangente positiva.
Relaciones entre las funciones trigonométricas en el tercer cuadrante
Las relaciones entre las funciones trigonométricas en el tercer cuadrante son cada vez más claras a medida que se profundiza en su estudio. La interacción entre el seno, el coseno y la tangente en este cuadrante es fundamental para comprender los valores negativos que adquieren.
Aplicaciones en problemas de la vida real
La comprensión de los valores negativos de las funciones trigonométricas en el tercer cuadrante es esencial en situaciones del mundo real, como el análisis de movimientos, el diseño de estructuras y la modelización de fenómenos naturales.
El concepto de amplitud y periodicidad
Es importante destacar que las funciones trigonométricas son periódicas, lo que significa que se repiten en intervalos regulares. Esta característica es esencial para entender cómo los valores negativos de estas funciones se manifiestan a lo largo de sus ciclos.
La influencia de la sinuosidad en el tercer cuadrante
La sinuosidad de las funciones trigonométricas en el tercer cuadrante es una manifestación clara de sus valores negativos. Esta cualidad es central para comprender cómo la variación de los ángulos afecta los valores de estas funciones.
Una mirada a la inversa de las funciones trigonométricas en el tercer cuadrante
La inversa de las funciones trigonométricas también juega un papel crucial en el análisis de sus valores negativos en el tercer cuadrante. Comprender la relación inversa conduce a una apreciación más profunda de cómo los valores negativos se relacionan con los ángulos.
El enfoque geométrico de los valores negativos
Una perspectiva geométrica en el estudio de los valores negativos de las funciones trigonométricas en el tercer cuadrante arroja luz sobre la naturaleza de las relaciones angulares y longitudinales.
La importancia en la educación matemática
La comprensión de los valores negativos de las funciones trigonométricas en el tercer cuadrante es esencial para los estudiantes, ya que sienta las bases para abordar conceptos más avanzados en matemáticas y física.
La exploración de los valores negativos de las funciones trigonométricas en el tercer cuadrante revela la complejidad y la importancia de estas funciones en el análisis matemático y su aplicabilidad en el mundo real. La comprensión de cómo estas funciones se relacionan con los ángulos en el tercer cuadrante es fundamental para abordar una amplia gama de problemas matemáticos y físicos.
Referencias
– Smith, J. (2018). Trigonometry in the Real World. Journal of Applied Mathematics, 10(2), 153-167.