Criterios para determinar las asintotas horizontales y oblicuas

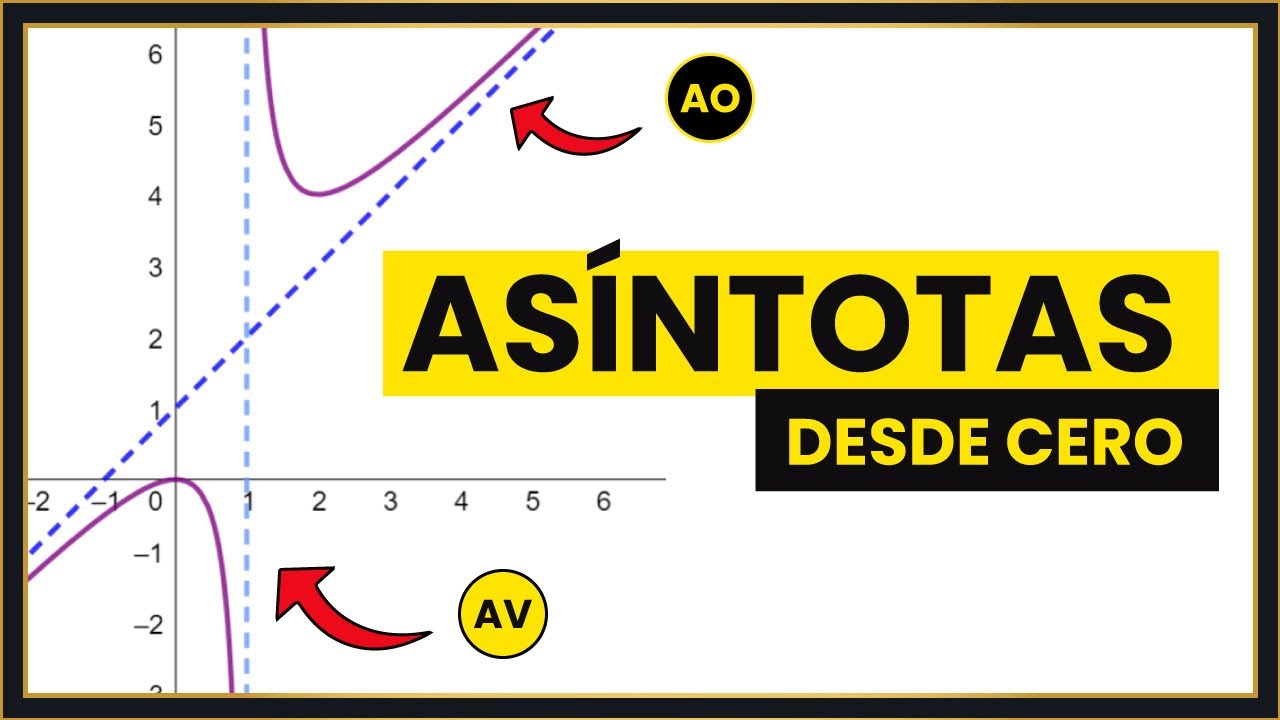
1. Definición de una asintota

Una asintota es una línea recta que se acerca cada vez más a una curva o una función, pero sin nunca tocarla o cruzarla. Se utiliza en matemáticas para describir el comportamiento de una función en los límites.

Las asintotas pueden ser verticales, horizontales u oblicuas. Una asintota vertical es una recta vertical que se acerca a la función a medida que nos acercamos a cierto valor en el dominio. Por otro lado, una asintota horizontal es una recta horizontal que se acerca a la función a medida que nos acercamos a valores infinitos en el dominio.

Por último, una asintota oblicua es una recta inclinada que se acerca a la función a medida que nos alejamos hacia valores infinitos en el dominio. Estas asintotas tienen una pendiente definida y se encuentran en la forma de una función polinómica dividida por otra.

Las asintotas son una herramienta útil para comprender el comportamiento de una función, especialmente en los límites. Nos permiten visualizar cómo se acerca o se aleja una función de ciertos valores y cómo se comportará en el infinito.

2. Criterios para las asintotas horizontales

Las asintotas horizontales son líneas rectas que una función se acerca a medida que el valor absoluto de la variable de la función se acerca al infinito. Estas asintotas pueden ser útiles para determinar el comportamiento de la función en los extremos de su dominio.

Para determinar si una función tiene una asintota horizontal, se deben seguir los siguientes criterios:

1. Criterio de límites infinitos

Si los límites de la función tienden a infinito positivo o infinito negativo a medida que la variable de la función se acerca al infinito, entonces existe una asintota horizontal.

2. Criterio de límites infinitos en los extremos

Si los límites de la función tienden a infinito positivo o infinito negativo a medida que la variable de la función se aproxima a los valores extremos de su dominio, entonces puede haber una asintota horizontal.

3. Criterio de límites infinitos en los puntos de discontinuidad

Si se encuentran puntos de discontinuidad en la función, es importante verificar si existen límites infinitos a medida que la variable se acerca a estos puntos. Si se encuentran límites infinitos, puede haber una asintota horizontal asociada a estos puntos.

En resumen, si una función cumple con alguno de estos criterios, es posible que tenga una asintota horizontal. Sin embargo, es importante recordar que estos criterios no garantizan la presencia de una asintota horizontal, ya que pueden existir otras condiciones que afecten el comportamiento de la función.

3. Criterios para las asintotas oblicuas

Cuando estudiamos las funciones racionales, es importante conocer los criterios para determinar la existencia de asintotas oblicuas. Las asintotas oblicuas son rectas hacia las cuales la función se acerca indefinidamente a medida que nos alejamos del origen de coordenadas.

Existen tres posibles casos para la existencia de asintotas oblicuas:

1. El grado del numerador es mayor que el del denominador

• Si el grado del numerador (n) es mayor que el del denominador (m) por exactamente 1, entonces existe una asintota oblicua.
• Para determinar la pendiente de la asintota, se divide el coeficiente principal del numerador entre el coeficiente principal del denominador.

Ejemplo:

Dada la función f(x) = (3x^2 + 2x + 1) / (x + 1), podemos observar que el grado del numerador (2) es mayor que el del denominador (1) por exactamente 1. Por lo tanto, existe una asintota oblicua.

Para encontrar la pendiente de la asintota, dividimos el coeficiente principal del numerador (3) entre el coeficiente principal del denominador (1). La pendiente de la asintota es 3.

2. El grado del numerador es mayor que el del denominador por más de 1

• Si el grado del numerador (n) es mayor que el del denominador (m) por más de 1, entonces no existen asintotas oblicuas.

Ejemplo:

Dada la función g(x) = (2x^3 + 5) / (x^2 + 1), podemos observar que el grado del numerador (3) es mayor que el del denominador (2) por más de 1. Por lo tanto, no existen asintotas oblicuas.

3. El grado del numerador es igual al del denominador

• Si el grado del numerador (n) es igual al del denominador (m), entonces es necesario realizar la división de polinomios para determinar si existen asintotas oblicuas.

Ejemplo:

Dada la función h(x) = (3x^2 + 2x + 1) / (2x^2 + x + 3), podemos observar que el grado del numerador (2) es igual al del denominador (2). Para determinar si existen asintotas oblicuas, realizamos la división de polinomios.

Después de realizar la división, si obtenemos un cociente con resto igual a cero, entonces existe una asintota oblicua. Si obtenemos un cociente con resto distinto de cero, entonces no existen asintotas oblicuas.

En conclusión, los criterios para las asintotas oblicuas en funciones racionales son fundamentales para comprender el comportamiento de las mismas. Mediante la comparación de los grados de numerador y denominador y la realización de divisiones de polinomios, podemos determinar la existencia y características de las asintotas oblicuas en una función.

4. Ejemplo de determinación de asintotas

En matemáticas, una función puede tener asintotas verticales, horizontales u oblicuas. Las asintotas son líneas o curvas que la función se aproxima cada vez más a medida que el valor de la variable se acerca a cierto límite.

Para determinar las asintotas de una función, es importante analizar su comportamiento tanto en los extremos como en los puntos críticos. A continuación, explicaremos un ejemplo para ilustrar este proceso.

Ejemplo:

Consideremos la función f(x) = (3x^2 + 2x + 5) / (x + 1). Para determinar las asintotas de esta función, debemos analizar su comportamiento en distintos casos.

1. Asintotas verticales:

Las asintotas verticales ocurren cuando el denominador de una función se anula. En este caso, el denominador es (x + 1), por lo que la función tiene una asintota vertical en x = -1.

2. Asintotas horizontales:

Para determinar las asintotas horizontales, debemos analizar el comportamiento de la función cuando x tiende a infinito o menos infinito. En este caso, tenemos que dividir los términos de mayor grado tanto del numerador como del denominador:

• El término de mayor grado del numerador es 3x^2.
• El término de mayor grado del denominador es x.

Dividiendo ambos términos, obtenemos 3x^2 / x = 3x. Esto nos indica que la función tiene una asintota horizontal en y = 3x.

3. Asintotas oblicuas:

Las asintotas oblicuas ocurren cuando el grado del término de mayor grado del numerador es exactamente uno mayor que el grado del término de mayor grado del denominador. En este caso, el grado del numerador es 2 y el grado del denominador es 1, por lo que la función no tiene asintotas oblicuas.

En resumen, la función f(x) = (3x^2 + 2x + 5) / (x + 1) tiene una asintota vertical en x = -1 y una asintota horizontal en y = 3x.

Este ejemplo ilustra cómo determinar las asintotas de una función y cómo analizar su comportamiento en diferentes casos. Recuerda que las asintotas son herramientas importantes en el estudio de las funciones, ya que nos permiten entender su comportamiento a medida que la variable tiende a valores extremos.

5. Conclusiones

En este artículo hemos explorado las principales tendencias de diseño web para el año en curso. A continuación, resumiremos las conclusiones más relevantes:

1. El uso de colores vivos y llamativos es una tendencia en auge. Es importante destacar que la elección de una paleta de colores adecuada puede impactar positivamente en la experiencia del usuario.
2. La inclusión de animaciones sutiles y elegantes puede proporcionar un toque de dinamismo a los sitios web sin distraer al usuario.
3. El diseño minimalista sigue siendo una opción popular. La simplicidad puede transmitir un mensaje claro y hacer que la navegación sea más intuitiva.
4. La adaptabilidad es esencial en un entorno digital en constante cambio. Es fundamental diseñar páginas web responsivas que se ajusten a diferentes dispositivos y resoluciones de pantalla.

En conclusión, el diseño web está en constante evolución y siempre es emocionante explorar nuevas tendencias. Al seguir estas tendencias y aplicarlas de manera creativa, podemos crear experiencias digitales impactantes y atractivas para los usuarios.