1. Introducción al triángulo rectángulo
En geometría, un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, un ángulo de 90 grados. Es uno de los tipos más comunes de triángulos y juega un papel importante en diversas ramas de las matemáticas y la física.
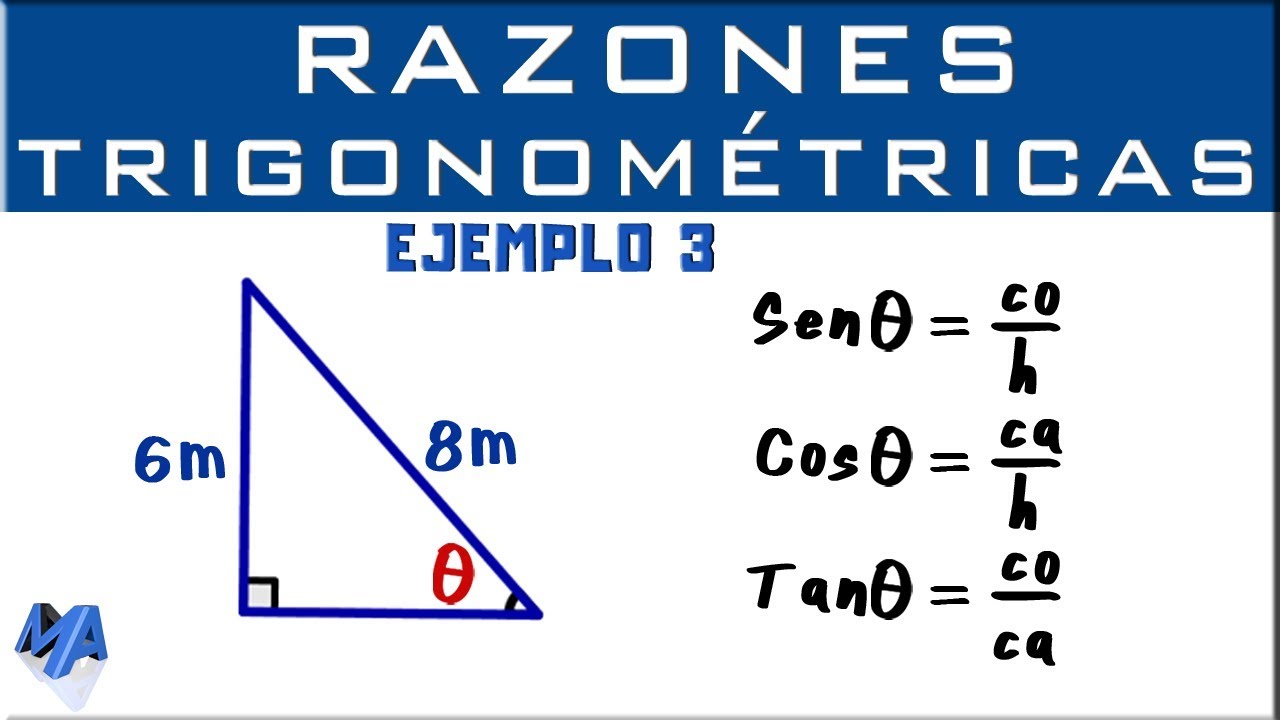
El triángulo rectángulo se caracteriza por tener tres lados, siendo el más largo la hipotenusa, que es opuesta al ángulo recto. Los otros dos lados se llaman catetos, siendo el cateto adyacente aquel que forma un ángulo con el ángulo recto y está junto a él, y el cateto opuesto aquel que está del otro lado del ángulo recto.
Para calcular diferentes propiedades del triángulo rectángulo, se utilizan las relaciones trigonométricas básicas, como el teorema de Pitágoras, que establece que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
Propiedades del triángulo rectángulo:
- Ángulo recto: El triángulo rectángulo tiene un ángulo de 90 grados.
- Hipotenusa: Es el lado más largo del triángulo, opuesto al ángulo recto.
- Catetos: Son los otros dos lados del triángulo, siendo uno adyacente y el otro opuesto al ángulo recto.
- Teorema de Pitágoras: Establece que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
El triángulo rectángulo es utilizado en diversos contextos, como la resolución de problemas de distancias y alturas, así como en cálculos de trigonometría y geometría analítica. Su estudio es fundamental para comprender conceptos más avanzados de geometría y matemáticas en general.
2. Definición del seno(a)
El seno es una función trigonométrica que se define como la relación entre el lado opuesto y la hipotenusa de un triángulo rectángulo. Se representa con la letra “a” y se calcula utilizando la ecuación sen(a) = a / h, donde “a” es el lado opuesto y “h” es la hipotenusa.
El seno es una medida angular que nos indica la proporción entre la altura de un punto en la circunferencia unitaria y el radio de la misma. Esta función trigonométrica oscila entre los valores -1 y 1, dependiendo del ángulo en cuestión. Si el ángulo es de 0 grados, el seno es 0, mientras que si el ángulo es de 90 grados, el seno es 1.
El seno es una de las funciones trigonométricas fundamentales y tiene diversas aplicaciones en áreas como la física, la ingeniería y la geometría. Además, es importante destacar que el seno es una función periódica, lo que significa que se repite a lo largo de la circunferencia unitaria.
En resumen, el seno es una función trigonométrica que relaciona el lado opuesto y la hipotenusa de un triángulo rectángulo. Se utiliza para medir la altura de un punto en la circunferencia unitaria y tiene aplicaciones en distintos campos de la ciencia y la matemática.
Características del seno:
- Función trigonométrica
- Relaciona el lado opuesto y la hipotenusa de un triángulo rectángulo
- Representado por la letra “a” en las ecuaciones
- Oscila entre -1 y 1
- Tiene diversas aplicaciones en física, ingeniería y geometría
- Función periódica con periodo de 360 grados o 2π radianes
3. Fórmula para calcular el seno(a)
El seno es una función trigonométrica muy utilizada en matemáticas y física. Nos permite calcular la relación entre el cateto opuesto a un ángulo en un triángulo rectángulo y la hipotenusa. La fórmula para calcular el seno de un ángulo a es la siguiente:
sen(a) = cateto opuesto / hipotenusa
Esta fórmula se basa en el Teorema de Pitágoras, que establece que en un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
Para obtener el valor del seno de un ángulo, se debe dividir la longitud del cateto opuesto a ese ángulo entre la longitud de la hipotenusa del triángulo.
Aquí hay un ejemplo para comprender mejor cómo se aplica la fórmula:
- Supongamos que tenemos un triángulo rectángulo en el cual el cateto opuesto mide 5 unidades y la hipotenusa mide 10 unidades.
- Aplicando la fórmula del seno, tenemos que:
sen(a) = 5 / 10 = 0.5
Por lo tanto, el valor del seno del ángulo a en este caso es 0.5.
Es importante recordar que el valor del seno siempre estará en el rango de -1 a 1, ya que es una función periódica que oscila entre estos dos valores.
En resumen, la fórmula para calcular el seno de un ángulo a es:
sen(a) = cateto opuesto / hipotenusa
¡Espero que esta explicación te haya sido útil para entender cómo calcular el seno de un ángulo!
4. Ejemplo de cálculo del seno(a)
El cálculo del seno de un ángulo es una operación trigonométrica comúnmente usada en matemáticas y física. El seno de un ángulo se representa como sin(a), donde “a” es el ángulo en radianes.
Paso 1:
Para calcular el seno de un ángulo, primero debes tener claro el valor del ángulo en radianes. Si el ángulo se encuentra en grados, puedes convertirlo a radianes utilizando la fórmula: radianes = grados * (π/180). Por ejemplo, si tienes un ángulo de 45 grados, se convierte a radianes de la siguiente manera: radianes = 45 * (π/180) ≈ 0.7854 radianes.
Paso 2:
Una vez que tienes el valor del ángulo en radianes, puedes utilizar una calculadora científica o una función trigonométrica en un lenguaje de programación para calcular el seno del ángulo. Por ejemplo, en JavaScript, puedes utilizar la función Math.sin(a) donde “a” es el valor del ángulo en radianes. Para nuestro ejemplo de 0.7854 radianes, el resultado sería sin(0.7854) ≈ 0.7071.
Es importante recordar que el resultado del cálculo del seno es un número entre -1 y 1, donde -1 representa el seno de -π/2 radianes y 1 representa el seno de π/2 radianes.
Ahora que conoces los pasos básicos para calcular el seno de un ángulo, puedes aplicar este conocimiento en ejercicios trigonométricos más complejos. La trigonometría tiene muchas aplicaciones en áreas como la física, la ingeniería y la navegación.
5. Conclusión
En la conclusión de este texto, encontramos varias frases importantes que resumen los puntos clave:
1. Resaltar los puntos principales
Es imprescindible identificar y resaltar los puntos principales del texto para que los lectores puedan captar fácilmente la información más importante.
2. Utilizar etiquetas HTML
Para resaltar las frases más importantes, podemos utilizar las etiquetas HTML <strong> </strong> dentro de los párrafos correspondientes.
3. Añadir encabezados y listas
Además de marcar las frases importantes, es útil utilizar encabezados como el <h3> para separar secciones y crear listas en HTML para organizar la información de manera clara y concisa.
4. Usar negritas
Otra opción para destacar frases importantes es utilizar la etiqueta HTML <b> para resaltar texto en negrita.
En resumen, para destacar las frases más importantes en nuestro texto, podemos utilizar etiquetas HTML como <strong> </strong>, encabezados y listas, así como negritas con la etiqueta <b>. Estas técnicas ayudan a mejorar la legibilidad y captar la atención de los lectores.