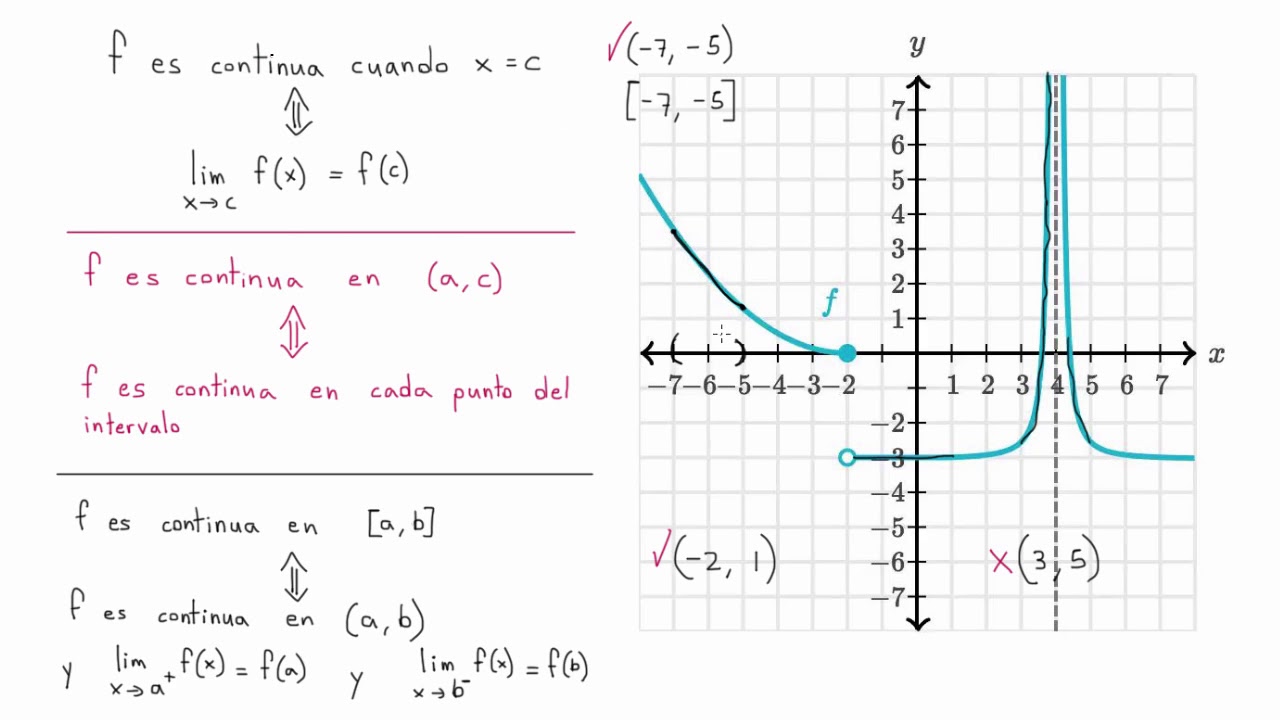
¿Qué significa la continuidad en un punto?
La continuidad en un punto es un concepto fundamental en el análisis matemático. La continuidad de una función en un punto indica que la función no presenta saltos, quiebres o discontinuidades en ese punto específico.
En términos más técnicos, podemos decir que una función es continua en un punto si el límite de la función cuando se acerca a ese punto es igual al valor de la función en ese punto. Esto implica que la gráfica de la función no tiene «agujeros» ni «saltos» en el punto en cuestión.
Existen diferentes tipos de continuidad en un punto. La continuidad ordinaria o de primer tipo se refiere a la continuidad comúnmente entendida, donde la función no tiene saltos ni quiebres abruptos. Por otro lado, la continuidad de segundo tipo se refiere a funciones que tienen saltos infinitos o discontinuidades más complejas.
Es importante mencionar también el teorema del valor intermedio, que establece que si una función es continua en un intervalo cerrado [a, b], entonces toma todos los valores intermedios entre f(a) y f(b). Esto significa que si una función es continua en un intervalo cerrado, no hay ningún punto en el intervalo en el que la función «se salte» algún valor.
Para determinar la continuidad en un punto, se deben cumplir tres condiciones: la función debe estar definida en ese punto, el límite de la función cuando se acerca a ese punto debe existir y ser igual al valor de la función en ese punto y el límite de la función debe ser finito. Si se cumplen estas tres condiciones, podemos asegurar que la función es continua en ese punto.
En resumen, la continuidad en un punto es una propiedad importante de las funciones, que indica que no presentan quiebres o saltos en ese punto en particular. Para determinar la continuidad en un punto, es necesario verificar que se cumplan las condiciones mencionadas anteriormente.
La continuidad en un intervalo y sus implicancias
La continuidad en un intervalo es un concepto fundamental en el análisis matemático. Este concepto nos permite describir el comportamiento de una función en un intervalo determinado.
Una función se considera continua en un intervalo si y solo si cumple las siguientes condiciones: en primer lugar, la función debe estar definida en ese intervalo. Además, la función debe tener límite en cada punto dentro del intervalo y el límite debe ser igual al valor de la función en dicho punto. Por último, el límite de la función cuando se acerca a un punto desde la izquierda debe ser igual al límite cuando se acerca desde la derecha.
La continuidad en un intervalo tiene algunas implicancias importantes. Por ejemplo, si una función es continua en un intervalo cerrado, entonces está acotada en ese intervalo. Esto significa que la función no tiene valores infinitos y se mantiene dentro de ciertos límites.
Otra implicancia de la continuidad en un intervalo es que permite utilizar el Teorema del Valor Intermedio. Este teorema establece que si una función es continua en un intervalo cerrado [a, b] y toma valores f(a) y f(b), entonces toma todos los valores intermedios entre f(a) y f(b). En otras palabras, la función pasa por cada punto del intervalo entre sus extremos.
En resumen, la continuidad en un intervalo es un concepto esencial en el análisis matemático. Permite describir el comportamiento de una función en un intervalo, establecer acotamiento y utilizar el Teorema del Valor Intermedio para obtener información adicional sobre la función.
Límites de una función y su relación con la continuidad
Una de las principales herramientas del cálculo diferencial es el concepto de límite. El límite de una función describe el comportamiento de la función a medida que su variable independiente se acerca a un cierto valor. Esta noción es fundamental en la comprensión de la continuidad de una función.
Límite de una función
El límite de una función f(x) cuando x tiende a un valor a, se denota como:
lim [ f(x) ] = L
x → a
Este límite se interpreta como el valor al cual se acerca la función f(x) a medida que x se acerca a a.
Existen tres casos posibles para los límites de una función:
-
Cuando el límite existe y es finito, es decir, L es un número real.
- En este caso, se dice que la función tiene un límite finito en el punto a.
-
Cuando el límite existe pero es infinito.
- En este caso, se dice que la función tiene un límite infinito en el punto a.
-
Cuando el límite no existe.
- Esto puede deberse a diferentes razones, como la función tiende a infinito, oscila entre diferentes valores o no se acerca a ningún valor específico.
Continuidad de una función
Una función se considera continua en un punto a si cumple las siguientes condiciones:
- El límite de la función en el punto a existe.
- El valor de la función en el punto a coincide con el límite.
- Los puntos aledaños al punto a también cumplen las dos condiciones anteriores.
En resumen, la continuidad de una función está estrechamente relacionada con la existencia y los valores de los límites en un punto. Si una función es continua en todos sus puntos, se dice que es una función continua en su dominio.
Explorando los diferentes tipos de discontinuidades
En el ámbito de las matemáticas y la física, las discontinuidades son puntos o regiones en los que una función o una operación presenta una interrupción abrupta o un cambio repentino. Estas discontinuidades pueden manifestarse de diferentes maneras y tienen características distintas.
Discontinuidades removibles
Las discontinuidades removibles son aquellas en las que la función está definida tanto a la izquierda como a la derecha del punto en cuestión, pero su valor es diferente en cada lado. Esto suele ocurrir cuando existe una discontinuidad en un punto, pero si se redefine la función en ese punto específico, se puede obtener una función continua y bien definida.
Discontinuidades de salto
Las discontinuidades de salto ocurren cuando la función tiene un salto finito en un punto, es decir, cuando los límites derecho e izquierdo existen, pero no son iguales. Esto significa que en el punto de discontinuidad, la función «salta» de un valor a otro sin pasar por todos los puntos intermedios.
Para representar una discontinuidad de salto, se puede utilizar la notación de corchetes: [x], donde «x» es el punto de discontinuidad.
Discontinuidades esenciales
Las discontinuidades esenciales son aquellas en las que la función no tiene límite en un punto específico. Estas discontinuidades suelen tener comportamientos caóticos y no se pueden eliminar mediante redefiniciones locales de la función.
Discontinuidades infinitas
Las discontinuidades infinitas ocurren cuando la función tiene un límite infinito en un punto específico. Esto significa que a medida que nos acercamos al punto de discontinuidad, la función se vuelve cada vez más grande o tiende a infinito.
Estos son solo algunos de los diferentes tipos de discontinuidades que se pueden encontrar en las funciones. Cada una de ellas tiene características y propiedades distintas, y son importantes para comprender cómo se comporta una función en puntos específicos. Explorar y comprender estas discontinuidades nos permite tener una visión más completa y detallada de las funciones matemáticas y físicas.
Aplicaciones prácticas de la continuidad y los límites
En el campo de las matemáticas, la continuidad y los límites son conceptos fundamentales que se utilizan de manera cotidiana para resolver problemas y desarrollar aplicaciones prácticas en diferentes áreas de conocimiento. Estos conceptos nos permiten analizar y comprender el comportamiento de funciones, modelos matemáticos y fenómenos naturales o físicos.
Análisis de funciones
Uno de los usos principales de la continuidad y los límites es en el análisis de funciones. Para determinar si una función es continua en un intervalo dado, es necesario evaluar los límites en los extremos de dicho intervalo. Esto nos permite identificar las discontinuidades y puntos de quiebre en la gráfica de la función. Además, los límites nos proporcionan información sobre el comportamiento asintótico de la función en diferentes puntos.
Optimización de procesos
La utilización de los límites en la optimización de procesos es otra aplicación práctica de estos conceptos. En el ámbito de la ingeniería, por ejemplo, se pueden utilizar límites para determinar el punto máximo o mínimo de una función que representa una variable de interés. Esto permite encontrar soluciones óptimas en diferentes situaciones, como la minimización de costos o la maximización de la eficiencia de un proceso.
Modelado y predicción de fenómenos naturales
La continuidad y los límites también son utilizados en el modelado y predicción de fenómenos naturales. Por ejemplo, en la meteorología se utilizan funciones matemáticas continuas para representar el comportamiento de la temperatura, la presión atmosférica o la velocidad del viento. Mediante el análisis de los límites de estas funciones, se pueden realizar predicciones sobre el clima o realizar estudios sobre pautas y tendencias.
Estudio de cambios y tasas de variación
El estudio de cambios y tasas de variación es otra aplicación importante de la continuidad y los límites. Al calcular el límite de una función en un punto específico, se puede determinar la tasa de cambio instantánea de dicha función en ese punto. Esto es fundamental en campos como la física, la economía o la biología, donde el análisis de las tasas de variación es esencial para comprender el comportamiento de diferentes variables y fenómenos.
En resumen, la continuidad y los límites tienen numerosas aplicaciones prácticas en diversos campos del conocimiento. Desde el análisis de funciones hasta el modelado de fenómenos naturales, estos conceptos nos permiten comprender y predecir el comportamiento de variables, optimizar procesos y realizar estudios detallados sobre cambios y tasas de variación. Su importancia radica en su capacidad para proporcionar herramientas matemáticas fundamentales para el análisis y la resolución de problemas en diferentes disciplinas.